MATh.en.JEANS 2001-2002 

Le sujet

Un polyèdre (du grec poly-, plusieurs et èdre, face) est un solide à plusieurs faces. Un polyèdre qu'on peut poser "à plat" sur une surface plane, sur n'importe laquelle de ses faces, est appelé convexe (du latin con-, avec, et vexus, tourné). Une fois posé, le polyèdre peut être basculé sur une autre face, par un mouvement de pivot autour d'une de ses arêtes, une culbute. En enchaînant des culbutes successives, on peut en quelque sorte le faire "rouler".

Nous vous proposons d'étudier les culbutes des polyèdres les plus simples : polyèdres réguliers et boites. Il s'agit de déterminer quelles configurations on peut obtenir par une série de culbutes et de comprendre comment on peut les obtenir.

• Quels emplacements peut occuper le solide ?
• Toutes les orientations sont-elle réalisables ?

A vous de choisir la situation qui vous intéresse le plus : le cas du dodécaèdre (voir ci-après la situation 1 et les premières pistes de réflexion) ou celui des boites rectangulaires (voir ci-après la situation 2)

 

Connus dès la plus haute Antiquité et décrits notamment par Platon, cinq polyèdres présentent un intérêt tout particulier. Ce sont les seuls polyèdres réguliers : ils ont le même aspect, quelque soit la face sur laquelle on les pose. Ces formes peuvent donc servir de dés parfaitement équitables.

 

tétraèdre (4 faces)	cube (6 faces)	octaèdre (8 faces)	dodécaèdre (12 faces)	icosaèdre (20 faces)
Offrant une bonne solidité et aisément construite par pliage, cette forme de berlingot, est encore utilisée pour le lait.	Facile à empiler, le cube est aussi la forme la plus courante des dés à jouer.	Cette forme cristalline naturelle du diamant se décompose en deux pyramides à base carrée.	La forme dodécaédrique est utilisée pour certains conteneurs d'ordures ménagères.	Structure de base de nombreuses architectures sphériques : trous sur une balle de golf, armatures de géodes ... Avec cette coloration de l'icosaèdre on reconnaît les pièces d'un ballon de football.

Premières pistes

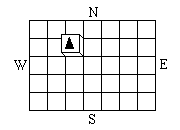
Un cube est à la fois une boite rectangulaire et un polyèdre régulier. En culbutant sur une surface plane, il occupe les cases d'un quadrillage. Il est commode d'utiliser les lettres N, E, W, S pour repérer le type de culbute effectué : vers le nord, l'est, l'ouest ou le sud. Essayez-donc la succession de 16 culbutes qui s'écrit EENNNWWSSEENNWSS. Trouvée par des collégiens de MATh.en.JEANS en 1991, elle permet d'imiter le glissement du cube d'une case en diagonale vers le nord-est : on retrouve à la fin la même orientation que l'orientation initiale. Il s'avère par contre impossible d'imiter par culbutes le glissement d'une seule case vers l'est (case B1) ou vers le nord (case B2). (Voir Les culbutos NEWS , article de collégiens, Actes MATh.en.JEANS, 1993)
Pour les polyèdres dont les faces sont des triangles équilatéraux, la situation est analogue à celle du cube: lors des culbutes, les faces se placent sur un réseau triangulaire et on peut utiliser trois signes (les symboles \ _ / ou les lettres T, E, R ... ) pour indiquer la direction des culbutes effectuées. Étant donnée un positionnement de départ, peut-on toujours trouver une série de culbutes qui amene le tétraèdre dans une position voulue ? Que se passe-t-il pour l'octaèdre ? Pour l'icosaèdre ?
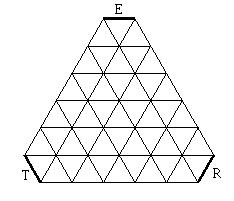Le dodécaèdre semble poser un problème à part : lors de culbutes successives, ses faces ne se placent pas suivant un réseau régulier simple de pentagones. Comment coder commodément une succession de culbutes ? Quelles sont les positions réalisables du dodécaèdre ?

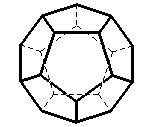
Configuration de départ.

Une grosse boîte d'allumettes est posée sur une table (de dimension 3cm x 6cm x 8cm par exemple). La face supérieure de la boîte (celle qui indique la marque), est bien au dessus, mais les inscriptions qu'elle porte sont à l'envers.

Votre objectif.

• Par une succession de culbutes bien choisies, remettre la boite à l'endroit, le plus près possible de son emplacement de départ.

Une suggestion : comme pour le cube, utilisez les lettres N, E, W, S pour repérer vos mouvements.

A quoi ça sert ?

Ces jeux de culbutes illustrent une vaste classe de problèmes de la recherche mathématique actuelle relevant de la théorie des groupes. Il s'agit :

- soit de combiner des opérations données afin de réaliser une transformation voulue.

- soit de reconnaître les "transformations neutres", c'est à dire les séquences d'opérations qui reviennent à ne rien faire ("problème des mots"). Savoir reconnaître de telles séquences permet de simplifier les expressions complexes qui correspondent à une combinaison de nombreux mouvements.

Documentation disponible sur ce sujet

Articles

• Extraits choisis (1 page) de l'article " Les culbutos NEWS " (article de collégiens, tous publics). Un cube roule sans glisser sur un damier, chaque face ayant exactement la taille d'une case ; une série de culbutes permettra-t-elle de l'amener à la case voulue avec l'orientation voulue ?
  Article complet : Les culbutos NEWS , Actes MATh.en.JEANS, 1993, p.169-173.
• Culbutos (collège Jean Vilar de Villetaneuse (93)), Actes MATh.en.JEANS, 1997, p.161-164. Un cube roule sur un damier, chaque face ayant exactement la taille d'une case ; peut-on, par une suite de basculements (culbutes) faire passer le cube (le culbuto) du coin Sud-Ouest du damier au coin Sud-Est, en retrouvant au dessus la même face dans la même orientation ?
  
• "Démonstration de la formule d'Euler. Polyèdres platoniciens". (Atelier "Exploration Mathématique" du lycée Louise Michel, 93 Bobigny). Actes MATh.en.JEANS, 1995, pp.55-62. Les polyèdres de Platon ne sont que 5. Pourquoi, comment ? Une lecture peut-être utile.

Contributions

• Sur les culbutes du tétraèdre (jumelage MATh.en.JEANS, école Bonis et collège Chopin, Melun,14 décembre 2001) Message du groupe d'écoliers de Melun et commentaires du chercheur.
  
• Quelques essais de retournement d'une boîte d'allumette par culbutes successives lors de la « Science en Fête » (Village des Sciences, Ministère de la Recherche, Paris, 19-20-21 octobre 2001). [Prochainement disponible, patience !]
• Retournement d'une boîte d'allumette par culbutes successives lors du 17ème Congrès MATh.en.JEANS(Cité des Sciences, Paris, 31 mars, 1-2 avril 2006). [jumelage Moirans-Pontcharra]

© MATh.en.JEANS 2001. Tous droits réservés.