Sujet n°1 : Communication sur une grille. [exposé]
Nb d'élèves : (4+2)(?)

Réussira-t-on à informer tout le monde en respectant les règles de communication en vigueur dans le réseau ?

Sujet 01L02 du LaboraToile. également traité par le jumelage Bordeaux-Le Taillan Médoc.

[Motivations : La diffusion rapide d'une information dans une ville, un pays, un réseau téléphonique, peut être organisée de bien des facons : le principe dit "du téléphone arabe" où chacun transmet la nouvelle à ses voisins est bien connu. C'est suivant le même principe que se propage le feu dans une forêt (à la différence essentielle près qu'un arbre brûlé ne transmet plus). La recherche des meilleures organisations possibles des transmissions dans un réseau relève de la théorie des graphes. Le problème particulier où l'on cherche à informer tout le monde en un minimum de temps est connu sous le nom de "problème des ragots".

L'étude systématique des propagations aléatoires, du type feu de forêt, utilise des techniques mathématiques variées : les probabilités, la théorie de la percolation (appelée ainsi à cause de la propagation de la vapeur dans la poudre de café) la théorie ergodique qui étudie notamment les zones d'un billard atteintes par une boule qui y circule indéfiniment et la théorie des équations aux dérivées partielles.]

Documentation disponible

Communication sur une grille (collèges l'Ardillière de Nézant à Saint Brice sous Forêt et Condorcet à Pontault-Combault). Actes MATh.en.JEANS, 1994, pp.45-50. [facsimilés version gif, version pdf]
Tous publics. Arithmétique et vecteurs pour diffuser l'information sur une grille,

Le réseau (module-recherche de Seconde technologique du lycée Pablo Neruda de Saint Martin d'Hères). Actes MATh.en.JEANS, 1995, pp.145-146.
Si le Vecteur est un agent de transmission d'une information entre points, quels seront les points informés ?

Communiquer dans une grille, par des élèves de troisième du Collège l'Ardillière de Nézant à St Brice sous Forêt (1997-98), Comptes-Rendus MATh.en.JEANS , n° 9801, 2000.

Sujet n°2 : Damiers et cannibales. [atelier]
Nb d'élèves : (2+2)(?)

[Deux joueurs posent alternativement des pions sur un damier ; aucune pièce n'est déplacée ; aucune de ses pièces ne doit être en prise par une pièce adverse. Un joueur perd s'il ne peut plus jouer. Qu'est-ce qu'une stratégie ? Peut-on gagner à coup sûr ?]

Documentation disponible

Damier et cannibales par Guillaume Akbaraly, Zeynel Anil, Zouhir Belbouab, Eric Nyamaku du Collège Victor Hugo de Noisy le Grand (93). Actes MATh.en.JEANS, 1997, pp.149-154.
Tous publics. Arithmétique et vecteurs pour diffuser l'information sur une grille,
[La brochure 997 est à commander à l'association]

Voici un extrait de cet article, donné cette année à Epinay comme énoncé de sujet :

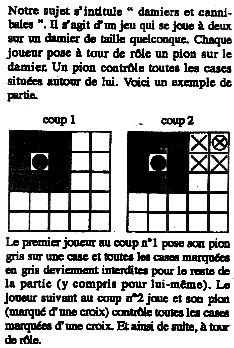
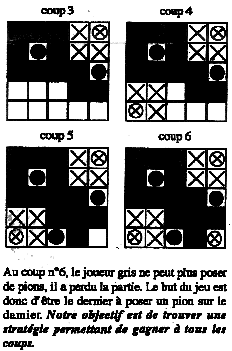
Sujet n°3 : Le réseau aérien. [atelier]
Nb d'élèves : 2 (?)

Le ministère des transports décide d'améliorer le trafic aérien français. Pour celà, il veut mettre en place entre un certain nombre n de villes françaises un réseau aérien qui vérifie les conditions suivantes:- le nombre de vols directs issus d'une ville donnée est le même pour toutes les villes du réseau.- un voyageur qui voudra aller d'une ville donnée à une autre en faisant au plus une escale aura exactement une possibilité d'un tel voyage. Pour quelles valeurs de n peut-on concevoir un tel réseau ?