|
Laboratoile MATh.en.JEANS. Année 2001-2002 |
|
Laboratoile MATh.en.JEANS. Année 2001-2002 |
|
|
Si l'on dispose d'un nombre illimité de plaques identiques, de forme carrée ou triangulaire, il n'est pas difficile de couvrir le plan tout entier sans perdre un seul cm2.
|
|
|
En effet, ces formes sont pavantes, c'est à dire qu'elles peuvent être juxtaposées exactement et indéfiniment. |
|
Avec des plaques identiques mais dont la forme est non pavante, on peut encore y parvenir sans trop de mal, en acceptant de superposer certaines parties des plaques (on négligera toujours leur épaisseur). On considère dans chacune des plaques une portion carrée, de la même taille pour toutes les plaques, puis on juxtapose ces carrés : certains endroits seront éventuellement couverts plusieurs fois mais tout sera bien couvert.
|
|
Un exemple prototypique est fourni par la question suivante :
|
|
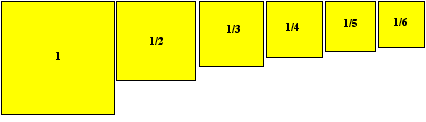 |
La forme la plus élaborée du problème, et la
plus intriguante, est celle du " jeu des carrés d'Eva",
où la seule donnée connue est la surface totale
disponible dans le stock : les plaques sont carrés mais non
seulement les tailles ne sont pas connues à l'avance, mais la
pose s'effectue plaque par plaque, dans un ordre lui aussi inconnu,
imposé par Eva...
|
Matériel : L'aire de jeu est le plan tout entier. Un sac (opaque) contient des plaques carrées jaunes en quantité inconnue, d'épaisseur négligeable. L'aire totale des carrés jaunes, notée A, est connue. But du jeu : L'objectif est de parvenir à couvrir complètement un carré rouge dont nous choisissons nous même, au début du jeu, la taille et l'emplacement. Notre score final sera l'aire de ce carré, soit s, si nous y parvenons, et nul sinon. Déroulement du jeu : A chaque tour Eva nous donne un carré jaune qu'elle puise dans le sac et nous plaçons ce carré où nous voulons. L'emplacement choisi est définitif : une fois posé, le carré n'est plus déplacé. Les carrés jaunes se trouvent ainsi placés un à un à notre guise : ils peuvent se chevaucher, et même se recouvrir. Le jeu se poursuit tant qu'il reste des carrés dans le sac. |
|
|
|
Entrées possibles
On peut étudier diverses variantes de ce jeu, plus ou moins simples à aborder.
|
|
|
|
|
|
|
|
|
|
|
A quoi cela sert-il ? ... un peu d'histoire
Ce problème ouvert est inspiré d'une fameuse conjecture géométrique (toujours ouverte, elle aussi) du mathématicien Hadwiger affirmant que
- tout domaine convexe plan peut être recouvert par 4 modèles réduitsde lui-même (ici, un modèle réduit est une figure obtenue par une homothétie de rapport k, 0 < k< 1) ,
- tout domaine convexe de l'espace peut être recouvert par 8 modèles réduits de lui-même.
- et, de manière générale, tout domaine convexe de l'espace réel à ddimensions peut être recouvert par 2dmodèles réduits de lui-même.
Vu que les homothéties préservent les directions des droites, il n'est pas très difficile de voir que, si cette conjecture de Hadwiger est vraie, le carré est un pire cas en dimension 2 (il faut 4 modèles réduits du carré pour le recouvrir), le cube un pire cas dans l'espace tridimensionnel (il faut 8 cubes modèles réduits du cube pour le recouvrir), et ... l'hypercube d-dimensionnel un pire cas dans l'espace à ddimensions (il faut 2d modèles réduits de l'hypercube pour le recouvrir). De là l'intérêt porté à la forme carrée dans le jeu d'Eva.
Actualité du sujet et documents
Disponibles au fur et à mesure de vos contributions dans
|
|
|
|
|
|