Approcher
, Les entiers de la forme
x2 + ay2
L'énoncé initial
des sujetsLa délégation "MATh.en.JEANS ":
Estelle, Rackibe et Amélie du Lycée Romain Rolland (95-Argenteuil), Gabriel (Collège Anne Frank, 77- Bussy Saint-Georges), Pierre Audin (Palais de la découverte, Paris), Pierre Duchet (CNRS, Paris) Mme Martine Fatin (Collèges Anne Frank, 77- Bussy Saint-Georges) et Mme Dominique Guy (Lycée Romain Rolland, 95-Argenteuil).
Sommaire
, Les entiers de la forme
x2 + ay2
L'énoncé initial
des sujets30 mars 2001, 11h45
|
|
" Typically, research consists in shaping many conjectures, exploding most of them, and establishing a few. " [Polyà] |
|
Approcher |
Collège Anne Frank Bussy Saint-Georges (77) |
|
 |
Le nombre
est compris
entre 1,4 et 1,5.Pour répondre à cette question, c'est un procédé ancien (l'antyphérèse) qui est ici mis à l'épreuve : en enlevant à un rectangle le plus grand carré possible on fait apparaître un autre rectangle, sur lequel on peut recommencer la même opération. |
|
Les entiers de la forme x2 + ay2 |
|
|
Estelle, Rackibe et Amélie ont étudié les nombres qui s'obtiennent en combinant deux carrés parfaits : ainsi le nombre 13 s'écrit 7x7-6x6 mais aussi 2x2 + 3x3 Elles ont notamment découvert que les nombres impairs et aussi les multiples de 4 pouvaient s'écrire comme différence de 2 carrés. |
 |
30 mars 11h45
Les sujets MATh.en.JEANS sont conçus pour une activité de recherche de longue durée (3 à 8 mois), finalisée par un congrès annuel et des publications. Ils mettent en scène des questions toujours vivantes dans les mathématiques contemporaines. Présenté oralement, ils sont présisés par un texte.
Sommes de deux carrés
Sujet proposé et suivi par Loïc Allys (Université du Maine, Le Mans). Atelier de Mme Dominique Guy (Lycée Romain Rolland, 95-Argenteuil)
Quels sont les nombres entiers de la forme x2 + ay2, avec a = -3, -2, -1, 1, 2 ou 3 ?
Le cas a = -1 est simple, les cas a = -3, -2, 2 ou 3 sont à l'identique.
Approcher (par
anthyphérèse)
Sujet proposé et suivi par François Parreau (Université Paris 13). Ateliers jumelés de Mme Martine Fatin (Collège Anne Frank, 77- Bussy Saint-Georges) et M. Hervé Grac. (Collège Condorcet, 77-Pontault-Combault)
Le nombre est apparu il
y a très longtemps par la géométrie : c'est le
rapport de la longueur de la diagonale à celle du
côté dans un carré ou, si on
préfère, la longueur de la diagonale du carré de
côté une unité. On se demande comment trouver la
valeur de cette longueur aussi précisément qu'on
voudra.
De nos jours, on imagine le plus
souvent les nombres non entiers par leur écriture
décimale, qui donne des valeurs approchées. On peut
aussi penser à approcher un nombre par des fractions : par
exemple, pour le nombre Pi, il est connu depuis longtemps que 22/7
est une bonne approximation, meilleure que 3,14. Pour chercher les
approximations de par des fractions, on propose de partir de la
méthode géométrique d'Euclide appelée
anthyphérèse par laquelle, sans doute, les Grecs
avaient déjà découvert que est
irrationnel, c'est-à-dire qu'il n'est pas égal à
une fraction.
Eux considéraient un nombre comme une longueur, ou plutôt comme le rapport des longueurs de deux segments. Dire que ce rapport est une fraction, c'est dire que les longueurs sont toutes deux multiples d'une même unité plus petite.
Si on ne connaît pas cette unité, on peut la trouver comme suit : on retranche le petit segment au grand. Le segment qui reste est encore un nombre entier de fois l'unité commune. On recommence avec ce reste et le petit segment, et on continue de même tant qu'on peut : le nombre total d'unités diminuant à chaque fois, on finit par avoir deux segments égaux et on a trouvé l'unité commune.
Essayez avec un rapport de 1,5 puis de 1,4. Une bonne façon de voir la méthode est de tracer un rectangle dont le rapport longueur/largeur est le nombre donné. En reportant la largeur sur la longueur, on divise le rectangle en un carré et un rectangle restant. Vous recommencez avec le rectangle restant... À la fin, il reste un carré et le côté de ce carré divise toutes les longueurs que vous avez construites, vous pouvez paver tous les rectangles avec le petit carré.
Maintenant essayez avec un rapport de
. Vous pouvez
partir d'une feuille de papier standard, format A4, et commencer la
construction en pliant le petit côté de la feuille sur
le grand. À quoi voyez-vous que le rapport hauteur/largeur est
précisément ?
À quoi voit-on que est plus petit
que 1,5 ? qu'il est plus grand que 1,4 ? Pouvez-vous montrer que le
découpage ne s'arrêtera jamais ? Qu'est-ce que cela
prouve ?
Pouvez-vous trouver des fractions
approchant mieux que 1,4 et 1,5 ? Encore mieux ?
POur plus d'informations sur ce thème : lire l'article de notre ami Benoît Rittaud, "Les irrationnels de Pythagore à Pac Man", Pour la Science n°294 (avril 2002), pp. 100-103.
30 mars 14h30-16h30
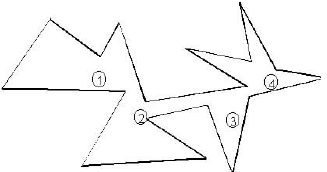
On veut surveiller un musée. Combien de gardiens seront nécessaires, au minimum ?
- La surface à surveiller sera délimitée par un polygone (ou plusieurs, s'il y a des obstacles)
- La position d'un gardien est indiquées par un point, intérieur à la surface du musée.
- Les gardiens peuvent voir tout autour d'eux mais ne se déplacent pas.
|
Pour ce musée 4 gardiens suffisent. Mais peut-être peut-on faire mieux : surveiller ce musée avec 3 gardiens seulement ou même 2 ? Qu'en pensez vous ? |
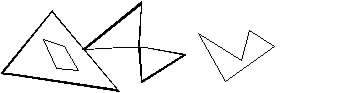Les musées modernes ont des forme de plus en plus
originales : peut-on trouver une méthode systématique
(par exemple un algorithme) qui donne une solution satisfaisante pour
des formes quelconques?
Plus d'informations : ce sujet est proposé dans le cadre du projet espace (sujet "espace" n° 42)
30 mars 14h30-16h30
Bébé ver de terre dort dans n'importe quelle position.
Voici quelques exemples :
Sa mère voudrait tricoter une couverture qui permette de le couvrir entièrement, quelle que soit la position du petit.
Par souci d'économie, elle voudrait que cette couverture soit de surface aussi petite que possible.
Pour simplifier : on prendra la longueur du bébé ver comme unité de longueur (1 décimètre = 10 cm dans le matériel fourni)
Plus d'informations : ce sujet est suivi par le LaboraToile depuis 2002 (sujet O2S2)
30 mars 14h30-16h30
|
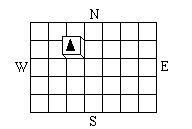
Le culbuto est un cube qui couvre exactement une case d'un quadrillage et qui peut être déplacé par culbutes successives. A chaque culbute, le culbuto bascule autour d'une de ses arêtes pour occuper une des cases voisines. Une face du cube comporte une flèche. |
| |
|
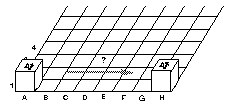
Le culbuto étant au départ sur la case A1, face marquée au dessus, flèche vers le Nord, peut-on l'amener par une succession de culbutes sur la case H1(montrée sur la figure) ou sur la case F1 (case en bas à droite pour les échiquiers 6¥6 qui sont fournis) tout en retrouvant à la fin la même face au dessus avec la flèche orientée vers le nord, comme si le culbuto avec glissé sans tourner ? Peut-on réussir pour d'autres cases ? | |
|
Parmi les pistes possibles :
| ||
|
Deux idées qui peuvent aider : 1) Pour mémoriser une succession de culbutes , on peut utiliser la boussole : par exemple, le mot EENNNWS indiquera que l'on fait deux bascules successives vers l'Est puis trois vers le Nord, puis deux à l'Ouest, puis une vers le sud. Avec un tel mot, si le cube était au départ sur la case A1, flèche audessus et vers le nord, il se retrouve sur la case B 3, flèche au dessus et vers l'ouest! 2) Les dimensions du quadrillage sur lequel on se déplace sont peut-être importantes : choisissez les à votre convenance petites, grandes, ou infinies... |
| |
Plus d'informations : ce sujet est proposé dans le cadre du projet espace (sujet "espace" n° 33)
L'objectif est l'émergence chez les élèves d'un rapport positif, dynamique et juste (pertinent et conforme aux usages) aux mathématiques et à leur objet. Au lieu d'apprendre avant de faire, on fait pour apprendre. Ce rapport se construit par l'usage, l'aboutissement et l'apprentissage d'une démarche scientifique.
L'espression "démarche scientifique" comprend la problématisation, l'objectivation et la représentation d'une situation, la formulation d'hypothèses et de lois, et une double validation, expérimentale et institutionnelle. Elle comporte en mathématiques des traits spécifiques : abstraction et conceptualisation, définition d'objets et fondement par hypothèses, type "interne" de la validation expérimentale.
Le sujet, présenté et motivé oralement (par le chercheur), doit être rapidement accessible avec un minimum de connaissances. Il s'appuie sur une problématique active dans les mathématiques contemporaines, tout en pointant une question source qui sert d'accroche à la recherche "novice".
Des séminaires bimestriels permettent l'échange sur un même sujet de plusieurs groupes (système de jumelage entre établissements) et une discussion critique (avec le chercheur et les animateurs).
Le problème est ouvert pour les élèves : même si la solution du problème est connue, elle suppose toujours un dépassement des connaissances initiales des élèves. L'énoncé et les directives des professeurs n'induisent ni méthode ni solution.
Ce sont le problème lui-même et les objets qu'il met en jeu qui constituent l'axe de référence permanent de l'activité : l'institution "École" et ses contraintes relatives aux savoirs sont neutralisés dans le travail de recherche proprement dit. Aucune restriction n'est imposée a priori quant aux outils utilisés. Le travail demandé est une contribution à la compréhension du problème, les résultats attendus étant des réponses partielles, des questions, des reformulations, des argumentations probantes, des faits expérimentaux, des "lois", des conjectures étayées. Ces résultats sont présentés de manière orale puis écrite (avec institutionalisation des apprentissages sur la preuve mathématique)
La progression de la recherche est placée sous la responsabilité des élèves eux-mêmes qui travaillent en petit groupes. Cela suppose des interventions adaptées de l'enseignant-animateur qui est plus "à coté" des élèves que face à eux. Le statut des activités est l'objet d'une (re)négociation constante : qu'est ce que chercher? Est-ce des mathématiques ?
MATh.en.JEANS à CINE-MATH-LILLE - 30 mars 2001
Le problème initial peut donner lieu à des variantes tout aussi intéressantes. Il peut également donner lieu à des sous-problèmes, c'est-à-dire des questions dont la résolution préalable semble nécessaire. Enfin, des cas particuliers peuvent sembler très intéressants : les résoudre peut être aussi difficile que de résoudre le problème initial, donc peut permettre la découverte de bonnes méthodes. Des variantes supplémentaires s'obtiennent en combinant les idées des variantes proposées.
- Partitionner une aire polygonale en un nombre minimum de régions convexes.
- Trouver pour une aire polygonale un recouvrement en un nombre minimum de régions, chacune pouvant être surveillée par un seul gardien.
- Etudier le cas des zones polygonales sans obstacle intérieur.
- Cas des musées à murs perpendiculaires.
- Etude en fonction du nombre de côtés.
- Un polygone (ou polyèdre) a-t-il toujours deux sommets qui se voient mutuellement ?
- Quelles sont les performances de l'heuristique "gloutonne" : on place un gardien à l'endroit d'où l'on voit un maximum de côtés (ou de coins, ou aire maximum...), on supprime la région surveillée et on recommence sur les morceaux restants.
- Comment calculer l'aire d'une figure polygonale, le volume d'un polyèdre ?
- Quel type de preuve peut-on imaginer pour établir que k gardiens ne suffisent pas pour une forme donnée ?
- Comment résoudre une combinaison logique de plusieurs inéquations ?
- Décomposer la forme en pièces et reformuler le problème en termes de carte plane.
- Classifier les formes où k gardiens suffisent pour k = 1,2,...
- Trouver les formes les plus "complexes" au sens où elles nécessitent un grand nombre de surveillants.
ou formes quasi-convexes avec 1 seul
trou.
Plus d'informations : ce sujet est proposé dans le cadre du projet espace (sujet "espace" n° 42)
MATh.en.JEANS à CINE-MATH-LILLE - 30 mars 2001