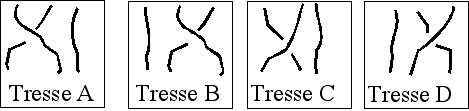
[Présentation des professeurs] Vous disposez de trois ficelles et vous ne savez faire que quatre types de tresses.

• Qu'est-ce qui se passe quand je combine mes tresses ?
• Est-ce que je suis capable de déméler une tresse que j'ai faite ?
• Est-ce que je suis capable de réaliser une tresse qu'on me propose ?

[Présentation de la rédaction] On part d'un premier terme (nombre avec des 0 et des 1). On définit un processus de fabrication pour le termes suivant, processus que l'on répète de proche en proche.

on cherche alors à comprendre

• la forme du terme général de la suite
• L'évolution de la "taille" de ce terme général la suite ..., autrement dit de sa longueur

Exemple.

Dans le cas de l'automate cellulaire ci-contre, le processus pour trouver une valeur consiste à faire la somme (modulo 2 : c'est à dire avec 1+1=0) de la valeur du dessus avec celle du dessus une case après.

[Présentation des professeurs] On sait que la loi de Newton entre deux planètes sphériques de masses m et m' est on prend G=1

Trouver la force dans le cas d'une planète sphérique de masse m et d'une planète cylindrique de masse uniforme m' et de hauteur e.

[Présentation des professeurs]. Déterminer (par équation) la courbe qui sépare le jour de la nuit sur une carte plane de la Terre.

Comment se déplace cette courbe avec les heures ? Et avec les saisons ? (Simulation sur un écran.)

[Présentation des professeurs] On trace deux cercles de centre (0;0,5) et (1;0,5) et de rayon 0,5. On souhaite placer entre ces cercles et l'axe des abscisses d'autres cercles tangents (à l'axe et aux autres cercles). On s'intéresse uniquement à l'abscisse des centres des cercles. Nous avons au départ F1={0;1}, puis F2={0;1/2;1} et ainsi de suite. Comment trouver les autres coordonnées ? Quelle est la logique dans la suite ? Quelles propriétés peut-on conjecturer (et démontrer) sur les termes de la suite ?

[Présentation des professeurs] On prend une fractale du type éponge ou triangle de Sierpinski.   Comment évolue le volume ou aire à chaque étape de la constrcution ? Ces grandeurs ont elle une limite ?

[Présentation des professeurs] Prenez une feuille de papier et pliez-la en deux (1° itération):
Repliez-la une seconde fois, sans déplier le premier pli, et dans le même sens (2° itération).
Ensuite, dépliez la feuille en laissant un angle de 90° entre les « faces » ainsi obtenues. En regardant la feuille de profil, vous obtenez un motif.
A vous de trouver le motif pour plusieurs itérations   et si possible sans faire l'expérience.

[Présentation des professeurs]	On suppose que l'avalanche est un rectangle de 1 sur 2. On part toujours du même point O. La victime est un point au hasard dans ce rectangle.
	Première étude possible: On se déplace horizontalement jusqu'à être à la perpendiculaire de la victime puis verticalement. On mesure la distance qu'on a fait d. On simule plusieurs fois l'expérience, quelle loi suit la distance d ?
	Deuxième étude possible: On choisi un angle au hasard (entre 0 et pi/2) fixé. On partira toujours avec cet angle. On va dans la "direction" de l'angle et on fait comme la fois d'avant. On mesure d. Quelle est la distance moyenne (en fonction de , la loi de d (en fonction de) ? La première étude correspond à la deuxième avec =0. On peut ensuite se poser le problème du meilleur choix de pour avoir la distance moyenne minimale .. et faire l'étude dans le cas d'une avalanche de dimensions a et b au lieu de 1 et 2.

• Peut-on couvrir un carré avec des carrés de coté entier, tous différents ?

Vous avez trois usines et trois maisons.

• Peut-on joindre chaque usine à chaque maison sans que les canalisations se croisent ?

• Quels objets géométriques peut-on construire seulement avec une règle et un compas ?

• Comment modéliser mathématiquement les embouteillages automobiles ?

retour liste des ateliers 2006