Sujet 1. Les amis de mes amis sont-ils mes amis [exposé]
nb d'élèves : 2 & 0

Considérons la proposition suivante : dans un groupe de six personnes, il est toujours possible d'en trouver trois qui se connaissent deux à deux (par exemple Anne et Bastien se connaissent, Bastien et Claire se connaissent, Anne et Claire se connaissent), ou trois qui ne se connaissent pas deux à deux (par exemple Damien et Étienne ne se connaissent pas, Étienne et Florence ne se connaissent pas, Damien et Florence ne se connaissent pas).

Cette proposition est vraie... mais sauriez-vous la démontrer ? Reste-t-elle vraie si l'on considère un groupe de 5 personnes ?

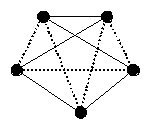
On peut modéliser graphiquement cette situation de la façon suivante : on dispose les personnes sur un cercle et on relie deux personnes par un trait plein si elles se connaissent et par un trait en pointillé si elles ne se connaissent pas (c'est plus joli avec deux couleurs, mais plus cher à imprimer...).

Par exemple :

En fait, cette figure répond négativement à la question concernant un groupe de 5 personnes : ici, nous n'avons ni trois personnes qui se connaissent deux à deux, ni trois personnes qui ne se connaissent pas deux à deux...

Qu'est-ce que trois personnes qui se connaissent deux à deux ? Un triangle en traits pleins ! Qu'est-ce que trois personnes qui ne se connaissent pas deux à deux ? Un triangle en pointillés !

Le dessin précédent est ce que l'on appelle un « graphe complet à 5 sommets » : il s'agit d'un graphe (dessin) dont les sommets représentent les personnes et tel que deux personnes quelconques sont toujours reliées par une « arête » (un trait) d'une certaine couleur (plein ou pointillé). Notre proposition peut alors s'énoncer de la façon suivante :

Dans un graphe complet à 6 sommets dont les arêtes sont coloriées à l'aide de deux couleurs, il existe toujours un triangle « monochrome » (c'est-à-dire colorié en une seule couleur).

Le graphe complet à n sommet se note généralement Kn. Ainsi, la figure précédente représente le graphe K5 et un triangle est en réalité le graphe K3 !...

Notre problème se généralise facilement et de nombreuses questions sont à ce jour sans réponse... On pourra par exemple se demander :

• à partir de combien de sommets est-on sûr de trouver un K4 monochrome ? un K5 monochrome ?
• à partir de combien de sommets est-on sûr de trouver deux triangles disjoints (sans sommets communs et sans arêtes communes, voir ci-dessous) monochromes ?
• à partir de combien de sommets est-on sûr de trouver un motif quelconque monochrome, par exemple le graphe X ci-dessous ?

Il est également possible de colorier le graphe complet avec 3 couleurs, voire plus... Dans ce cas, on peut alors se demander :

• à partir de combien de sommets est-on sûr de trouver un triangle monochrome dans un graphe complet colorié avec 3 couleurs ? avec 4 couleurs ?

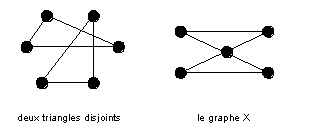
Indiquons pour finir de quelle façon de tels résultats peuvent être obtenus en prenant pour exemple notre problème initial des six personnes... Pour montrer que 6 est la bonne réponse à la question « à partir de combien de sommets est-on sûr de trouver un triangle monochrome dans un graphe complet colorié avec deux couleurs ? », il faut :

• montrer que quelle que soit la façon de colorier le graphe K6 avec deux couleurs, il apparaît toujours un triangle monochrome...
• montrer que 6 est la meilleure solution en montrant qu'il existe une coloration du graphe à 5 sommets sans triangle monochrome (ce que nous avons fait précédemment...).

Sujet 2. La stratégie des allumettes [sujet abandonné]
nb d'élèves 4 & 0;

Il existe de nombreux jeux d'allumettes et celui qui nous intéresse est le suivant : deux joueurs disposent d'un tas de 50 allumettes et retirent à tour de rôle un certain nombre d'allumettes.

Le premier joueur peut retirer 1 ou 2 allumettes du tas.
Lorsqu'un joueur a retiré n allumettes, le joueur suivant peut en retirer au maximum 2n.
Le joueur qui retire la dernière allumette est déclaré perdant.

Le problème qui nous intéresse est le suivant.

• Existe-t-il une stratégie gagnante pour le premier joueur ? pour le deuxième joueur ?
  ... et si oui laquelle ?

La technique à mettre en oeuvre est une technique classique en théorie des jeux, qui consiste à déterminer les « positions gagnantes »... Une « position » est une information qui permet de décrire la situation du jeu au moment où l'un des joueurs doit jouer. Dans notre exemple, une position peut être représentée par un couple (a,b), où a représente le nombre d'allumettes restant dans le tas et b le nombre d'allumettes retirées par le joueur précédent (on sait ainsi que l'on pourra retirer entre 1 et 2b allumettes).

Il est facile de se convaincre par exemple que (1,b) est toujours une position perdante (il reste une allumette, on a donc perdu) alors que (2,b) est toujours une position gagnante (en enlevant une allumette, on conduit l'adversaire à une position perdante...).

Ainsi, une position perdante est une position qui ne permet jamais de gagner (on suppose que l'adversaire ne commet jamais de faute) et une position gagnante est une position qui envoie l'adversaire dans une position perdante... simple, non ?

Notre problème consiste alors à répondre à la question suivante :

• Quelles sont les positions gagnantes ? et, en particulier, (50,1) est-elle une position gagnante ?
  (Remarquons que (50,1) modélise bien la position initiale car le premier joueur peut retirer 1 ou 2 allumettes...)

  La méthode à suivre peut être la suivante :

  • Considérer dans un premier temps un nombre plus faible d'allumettes (avec 1 ou 2 cela doit être trivial !).
  • Essayer de deviner comment se déterminent les positions gagnantes (et perdantes !).

  On pourra également considérer différentes variantes de ce jeu, selon l'inspiration :

  • on peut par exemple supposer qu'il y a au départ 2 tas de 25 allumettes et qu'à chaque étape les allumettes retirées par un joueur doivent appartenir à un même tasŠ

Sujet 3. Les commentaires du mathématicien [exposé]
nb d'élèves 0 & 4;

Il s'agit d'étudier une suite de caractères :

1

11

21

1211

111221

312211

...

Le secret ? : chaque ligne est en fait constitué de la "lecture" de la ligne précédente...

Documents. Ce sujet fut traité à plusieurs reprises par les ateliers MATh.en.JEANS, sous une forme plus ou moins générale. Trois articles sont disponibles :

La suite de Conway (version pdf) par des étudiants du module MATh.en.JEANS de l' Université d'Aix-Marseille II en 1995, Actes MATh.en.JEANS 1995, pp 153-158. (Brochure disponible sur commande)
Les suites de Conway (version pdf), par le jumelage MATh.en.JEANS du collèges J. Vilar de Villetaneuse et des kycées Jacques Feyder d'Épinay et Paul Éluard de St Denis en 1996-97, Actes MATh.en.JEANS 1997, pp 9-11. (Brochure disponible sur commande)
La suite de Conway (version pdf), par des étudiants du module MATh.en.JEANS de l' Université d'Aix-Marseille II en 1997, Actes MATh.en.JEANS 1997, pp 11-17. (Brochure disponible sur commande)

Un sujet voisin, les mots de Kolakoski, concerne les suites "autoréférentes" , c'est à dire les suites infinies de chiffres qui coïncident avec leur propre lecture. Il a été proposé par le LaboraToile en 2002.