Sujet 1 : Décomposition de grilles en composantes connexes [exposé]
nb d'élèves : 5 & ? (Georges GOETZ (2^de), Emilie-Sophie NOBLE (TS), Sébastien POUZOLS (TS), Stéphan ROSSIS (2^de); ?)

Un graphe est un ensemble de points (appelés sommets) et de lignes (appelées arêtes) reliant des paires de points.

On s'interesse ici à des graphes particuliers, appelés grilles, donnés par un nombre de lignes et de colonnes. On notera G(l,c) le graphe composé de l lignes et c colonnes.

Le problème consiste à déterminer le nombre de façons différentes de décomposer une grille de taille donnée G(l,c) en un nombre donné p de composantes connexes (voir figures) et en utilisant un nombre donné d'arêtes.

On notera N(l,c,p,q) ce nombre.

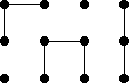Un sous-graphe d'une grille G(3,4)

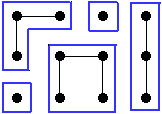Les 5 composantes connexes de ce sous graphe

Sujet 2 : Coloration des grilles orientées [exposé]
nb d'élèves 7 & ? (Julien BONNEAU, Jonathan BIMBERT, Pascal ENCINAS, Olivier GAZEAU, Arnaud LEMPEREUR, Mathieu RAMBAUD, Julien REY, (1S);

Un graphe est un ensemble de points (appelés sommets) et de lignes (appelées arêtes) reliant des paires de points. On s'intéresse ici à des graphes particuliers, appelés grilles, donnés par un nombre de lignes et de colonnes. On notera G(l,c) le graphe composé de l lignes et c colonnes.

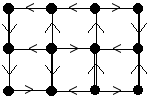
On considère ici des orientations de la grille, obtenues en orientant chaque arête d'un des sommets extrémités vers l'autre (nous avons deux possibilités pour chaque arête). Les arêtes ainsi orientées sont appelées arcs.

On souhaite maintenant « colorier » les sommets des grilles orientées avec des entiers : 1, 2, 3, etc., de façon telle que :

- les sommets voisins (reliés par un arc) ont des couleurs distinctes,
- pour toute paire de couleurs a et b, les arcs reliant les sommets de couleur a aux sommets de couleur b ont tous la même direction (tous de la couleur a vers la couleur b, ou tous de la couleur b vers la couleur a).

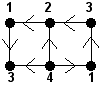Une coloration autorisée

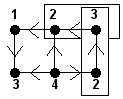Une coloration interdite : 2 vers 3 et 3 vers 2

• Le problème est de trouver le nombre minimum de couleurs nécessaires pour colorier ainsi les grilles orientées.

[Note de la rédaction : la problématique générale de la coloration de graphes, est abordée sous d'autres formes à Cestas et Mérignac (1). St-Orens de gameville et Toulouse, et Cluses et Paris (1).]

Sujet 3 : Coloration de brins [exposé]
nb d'élèves : 3 & ? [Fabian BILLAUT (TS), Pascale ENCINAS (2nde), Edouard EWANS (TS)]

Un graphe est un ensemble de points (appelés sommets) et de lignes (appelées arêtes) reliant des paires de points.

On souhaite maintenant colorier des « demi-arêtes » appelées brins. Ainsi chaque arête aura deux couleurs, placées sur les côtés opposés de l'arête. On utilise les entiers pour désigner les couleurs : 1, 2, 3, etc.

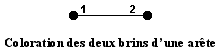
Les contraintes de coloration sont les suivantes

• les deux brins d'une même arête (brins opposés) doivent avoir des couleurs distinctes (A),
• deux brins entrants dans le même sommet (brin voisins) doivent avoir des couleurs distinctes (B)
• deux brins tels que l'un entre dans le le même sommet que le brin opposé de l'autre (brins adjacents) doivent avoir des couleurs distinctes (C).

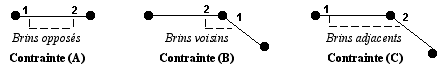
Le problème est de colorier les brins d'un graphe en utilisant le moins possible de couleursŠ