Thèmes de recherche possibles suggérés au moment du choix du sujet (dans le classeur) :

&emdash; jeux de symétrie sur les chiffres, lettres, mots ; exemples de graphismes spéciaux permettant d'introduire des symétries dans l'écriture.

&emdash; définitions diverses des différentes symétries possibles pour un dessin. Classifications.

&emdash; utilisation des symétries d'une figure pour démontrer certaines de ses propriétés.

&emdash; utilisation pour déterminer une stratégie gagnante à coup sûr dans certains jeux.

Thème de recherche proposé après le choix du sujet (négociations avec le groupe, en fonction du début d'avancement du travail) :

Chercher toutes les symétries laissant invariante globalement une figure donnée.

exemples possibles :

• triangle isocèle
• triangle rectangle isocèle
• triangle équilatéral
• rectangle
• parallélogramme
• losange
• trapèze quelconque
• carré

Exemples d'écrits du groupe : (rédigés et brouillons)

définition du dictionnaire.

[symétrie: ] disposition de deux figures se correspondant point par point, de telle sorte que deux points homologues soient à égale distance d'un point, d'une droite, ou d'un plan.

Palindromes : Un palindrome est un mot que l'on peut lire indifféremment de la droite vers la gauche ou dans l'autre sens.
ex : LAVAL = LAVAL.
Le plus long est Saippuakivikauppais (19 lettres) en finnois = marchand de savon. Le malagalam est le nom de la langue parlée par les Mayali au Kerala dans le sud des Indes.

Certains fonds baptismaux en Grèce et en Turquie portent l'inscription circulaire suivante:
NI ON ANOMHMATAMH MONAN O IN
ce qui signifie : "Ne lave pas seulement mon visage mais aussi mes pêchés".
La phrase « Eric notre valet alla te laver ton ciré » compte 32 lettres ; un des exemples les plus célèbres :
« Tu l'as trop écrasé, César, ce port-salut », 31 lettres.

Symétrie par rapport à une droite :

définition : deux points M et M' sont symétriques par rapport à une droite D si cette droite est médiatrice du segment [M, M'] c'est-à-dire qu'elle soit perpendiculaire au segment [M, M'] et passe par son milieu.

Soit D une droite appelée "axe de symétrie". Soit M un point n'appartenant pas à D. Il existe un point I D tel que [MI] soit perpendiculaire à D. Le prolongement de [MI] s'appelle [Ix). Il existe alors un point M' de [Ix) tel que [MI] et [IM'] soient de longueur égale.

Les points M et M' sont symétriques par rapport à D.

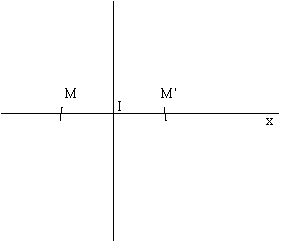Symétrie par rapport à un plan :

Deux points M et M' sont symétriques par rapport à un plan P lorsque ce plan est le plan médiateur du segment MM'.

Remarque.

les symétries par rapport à un point et par rapport à un plan transforment un segment AB en un segment égal A'B'.

Comptes Rendus MATh.en.JEANS 91-01 

© MATh.en.JEANS 2003. Tous droits réservés.