Accueil MATh.en.JEANS

1 L'opération MATh.en.JEANS

MATh.en.JEANS est l'acronyme de " Méthode d'Apprentissage des Théories Mathématiques en Jumelant des établissement pour une Approche Nouvelle du Savoir ". L'objectif est la popularisation des mathématiques vivantes en milieu scolaire et universitaire par la valorisation des résultats et surtout des méthodes de la recherche.

En mettant les jeunes en liaison avec des mathématiciens et aux prises avec d'authentiques problèmes issus de la recherche actuelle, "MATh.en.JEANS" inverse la tendance courante de la classe de mathématiques et assigne à l'enseignant un rôle différent.

Pour se lancer dans l'étude, il n'est plus nécessaire de posséder d'avance tous les outils et la démarche de résolution n'est plus détenue par le maître. Certitudes et réponses cèdent la place au doute, au questionnement et à la découverte. Loin d'être réservée à une élite, l'activité s'adresse à tous : c'est par la représentation, le débat critique et la communication que se forgent les connaissances et s'affirment les capacités créatrices.

Ingrédients types du "jumelage MATh.en.JEANS"

Un(e) mathématicien(ne), deux établissements (école, collège, lycée, université); dans chacun, un enseignant et une vingtaine d'élèves choisissant cette activité ; un bouquet de sujets à la fois attractifs et sérieux ; une "méthode" pédagogique et un calendrier prévoyant, sur l'année, un atelier hebdomadaire (travail collectif en petit groupes de 1h30 à 2h) , 4 "séminaires" réunissant tous les participants, et une présentation "officielle" des résultats (communication en congrès + article).

L'association "MATh.en.JEANS".

Lancée par une action pilote en 1989-90 dans le cadre d'une reprise de l'initiative ministérielle "1000 classes-1000 chercheurs", l'opération MATh.en.JEANS s'est doté d'un statut associatif pour mieux coordonner des aides spécifiques qu'elle obtient de ses partenaires (MESR en 1990 et 91, CNRS, projets d'établissements, aides à l'innovation pédagogique et l'action éducative, soutiens académiques de l'Éducation Nationale, Ateliers de Pratique Scientifique, collectivités territoriales, éducation prioritaire...

L'Association MATh.en.JEANS (AMeJ) coordonne des actions de terrain et organise un congrès annuel avec actes (350 participants cette année dont 250 jeunes). Elle poursuit la réflexion théorique et l'expérimentation, assure la promotion de la "méthode", dispense des formations nationales et académiques et réalise des projets pédagogiques spécifiques (les projets "Chryzode" (1995) et "Espace" (1996) ont bénéficié d'une aide du ministère).

L'association a reçu le prix de la démarche scientifique (salon PÉRIF 1990) et le prix d'Alembert (SMF, 1992). Elle est parrainée notamment par la Société Mathématique de France (SMF) et l'Association des professeurs de Mathématiques de l'enseignement Public (APMEP). Elle fut initiatrice et partenaire des congrès satellites juniors qui se tiennent maintenant régulièrement en parallèle des Congrès Mathématiques Européens. Elle a permis à de jeunes talents de se révéler (ainsi de Yann Ollivier, 1er prix du Concours Européen du jeune scientifique en 1996) et à plus de 2000 jeunes de vivre les mathématiques avec ... plaisir !

2) Quelques remarques sur la situation particulière des ateliers "MeJ" en ZEP

Résultats spécifiques obtenus

Les ateliers MATh.en.JEANS placent les élèves dans une dynamique de projet dont ils sont les principaux concepteurs et les artisans responsables. Pour cette raison ils sont adaptés à tous les élèves, quelque soit leurs niveaux scolaires.

La maîtrise des résultats obtenus en ZEP/REP, même s'ils montrent parfois des progressions spectaculaires, s'avère conforme à nos attentes : elle est tout à fait comparable à celle obtenue dans les autres établissements. Si le "niveau" des résultats obtenus reste fortement corrélé aux connaissances antérieures des élèves, la créativité des enfants et leur implication nous semblent en revanche légèrement supérieure en ZEP à celle des autres ateliers.

Une des raisons essentielles du bon fonctionnement des ateliers MATh.en.JEANS en zone d'éducation prioritaire réside dans l'accent qui y est mis sur la communication et l'échange (entre élèves d'un même groupe, entre groupes distant, entre établissements différents, entre élèves et adultes mathématiciens). Les progrès dans l'expression orale et écrite, dans l'éveil de la curiosité et le souci de conceptualisation sont très sensibles. L'atelier de mathématiques est très souvent la première occasion pour les élèves d'apprendre à travailler en groupe (mais cette observation n'est pas spécifique aux ZEP).

Principales difficultés rencontrées

Elles sont de nature parfois idéologiques, souvent matérielles :

- Le caractère innovant et ambitieux des activités proposées (de la vraie recherche mathématique !) heurte parfois des habitudes ou des convictions solidement établies. Faute de temps, il n'est pas souvent possible de mener à terme les explications, les discussions préalables et le travail de concertation nécessaire avec les équipes éducatives concernées.

- Les enseignants ne sont pas préparés "naturellement" à ce genre d'activité. Une formation est nécessaire, qu'il est difficile d'assurer (insuffisance de moyens horaires et budgétaires pour les enseignants concerné, absence de décharge pour les formateurs de l'association MATh.en.JEANS).

- Les emplois du temps des établissements ne sont pas adaptés à un fonctionnement optionnel ou périscolaire. Difficulté de mise en oeuvre de véritable ateliers mélangeant des niveaux et des classes différentes.

Atelier en club ou en classe entières ?

- Le fonctionnement d'une activité non imposée, avec des élèves volontaires de niveaux et de classes différents est, pédagogiquement le plus souhaitable et le plus simple à mettre en oeuvre. La forme "Atelier scientifique" (en partenariat avec un organisme de recherche) est bien adaptée à ce cas. Outre les problèmes d'organisation pratique que cela entraîne, ce type de fonctionnement suppose une reconnaissance institutionnelle et, dans les conditions actuelles, un allongement du service pour l'enseignant, qui, souvent, regrette de ne pas s'adresser à tous les élèves.

- Le fonctionnement au sein d'un classe est possible mais suppose un effort particulier de formation pour les enseignants et les partenaires ainsi qu'une implication forte. La démarche suivie en atelier est en effet en rupture avec la présentation traditionnelle des savoirs et la notion usuelle de programme. D'où allongement du temps de préparation pour les professeurs et réaménagement nécessaire de l'horaire des élèves dans la discipline (effectifs réduits, heures consécutives).

3) Établissements concernés et thèmes d'activités (1997-2000)

(Les établissements classés en ZEP ou Zone sensible sont en gras.)

Écoles primaires en Maine et Loire : écoles Jean-Jacques Rousseau et Charles Bénier (Angers); écoles Jacques Prévert (Saumur) et du Dolmen (Bagneux)

Projet en classe entières (cycle 3).Contact : Jean Mainguené; Chercheur Pierre Duchet et Jean Mainguené

Voir publication

(1) Les couleurs de Guthrie.

Le problème du coloriage d'une carte de géographie avec le moins de couleurs possible : les pays frontaliers doivent être de couleurs différentes.

(2) Les balances de Jullien.

Peser des nombres pour les écrire : inventer son propre système de numération.

(3) Le cavalier d'Euler

Problème ancien du voyageur de commerce moderne : avec un cavalier sur un échiquier, passer dans le plus d'endroits possible sans repasser deux fois au même endroit.

(4) Les tresses d'Artin

Comment dénouer une tresse par addition d'une autre tresse ?

(5) Les pentaminos paveurs.

Avec des morceaux d'échiquier comportant 5 cases, comment fabriquer un carreau de forme compacte ?

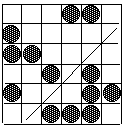
(6) Des pions et des lignes.

Un damier contient 4 types de lignes : horizontales, verticales et diagonales (montantes ou descendantes). Il s'agit de "surveiller" toutes les lignes en disposant un minimum de pions : on souhaite que chaque ligne contienne une case au moins qui soit occupée par un pion.

13 pions disposés comme cela ne suffisent pas : une ligne n'est pas surveillée.

12 pions disposés ainsi conviennent

Réussirez-vous avec moins de pions ? ...Encore moins ? ...Et si le damier était plus grand ? ...Plus petit ?

Collège Victor Hugo (94-Noisy le Grand) et Collège Condorcet (Pontault-Combault)

Contact : Pierre Lévy.Chercheur :Olivier Bodini.( 11 élèves participants)

Le collège avait toutes les conditions pour être classé "ZEP" mais ne le fut qu'en 99.

Sujet 1   Comment flotte un bouchon ?

Un bouchon flotte-t-il "debout", à la manière d'un pion de dame, ou "couché", à la manière d'un tronc d'arbre ?

Sujet 2   Le centre de la France.

Comment définir et trouver le centre de la France ?

Sujet 3  Le chemin le plus rapide.

Trouver une trajectoire qui permet à une bille de rouler le plus vite possible d'un point à un autre situé plus bas que lui, les deux points n'étant pas sur la même verticale.

Sujet 4   Le meilleur lieu de rendez-vous.

Étant donnés trois points A, B, C, trouver le point D tel que la somme des distances AD + BD + CD soit minimale. Généralisation à un nombre quelconque de points.

Collège Elsa Triolet (93-SAINT DENIS)

Contact M. Adrien FRYC, Mme "Muriel" "LEPROVOST". Chercheur François Parreau.

Sujet 1   Les nombres au hasard.

Comment s'assurer qu'un nombre est bien "au hasard" ? Peut-on en construire ?

Sujet 2  Problème du verger.

Un verger est composé d'arbres de diamètres égaux donnés, placés sur les noeuds d'un quadrillage régulier. Quels sont les arbres vus par un observateur placé à l'origine (seul noeud du quadrillage où il n'y a pas d'arbre) ? Quel est l'arbre le plus éloigné qu'il peut voir ?

Sujet 3   Le jeu du "cogitarium".

Autour d'un cercle, on place n cases et, pour commencer, un pion par case. Le joueur (solitaire) déplace à chaque coup, deux pions, pris dans une même case ou non, d'une case, l'un dans un sens, l'autre dans l'autre. Tous les pions doivent arriver dans la même case. Existe-t-il des stratégies "gagnantes" ?

Collège Molière (94 "IVRY" SUR SEINE)

Parcours différencié (classe de 5ème). Contact : Hélène Kraeutler ; Chercheur Jean-Gabriel Attali

sujet 1 Les écrans

Étude et description des parties convexes, étoilées, "flexées"

Recherche d'écrans particuliers Peut-on trouver un semi-écran qui permet d'observer sans être vu?

Sujet 2   Pavages de rectangles

Quels sont les rectangles que l'on peut paver avec des morceaux d'échiquier formé de quatre cases disposées en "L" ?

Lycée Romain Rolland (95-Goussainville) (zone sensible)

Contact Mme Jacqueline Durlewanger. Chercheur Stéphane Labbé

Sujet 1   Duplication du cube

Comment construire un cube de volume double du cube donné ?

Sujet 2   Géométrie sur une sphère

La terre est ronde comme un ballon. Comment aller tout droit ? Comment y faire de la géométrie ?

Sujet 3   Découpage de polygones

Est-il possible de transformer, par découpage et réassemblage de morceaux, un polygone en n'importe quel autre polygone d'aire égale ?

Sujet 4   De rebonds en rebonds

Comment se comporte une balle rebondissant sur une surface quelconque ? Va-t-elle s'"arrêter" ? Jusqu'où ira-t-elle ? Le but est d'étudier la suite décrite par les impacts successifs de la balle sur la surface. Converge-t-elle ? Par quels paramètres son comportement est-il régi ?

Lycée Jean "Macé" (94-Vitry sur Seine) (zone sensible)

Atelier Scientifique. Contact : Karine Van Effenterre ; Chercheur : J.-G. Attali ?

"Priz de tête" sur une roue de vélo.

Comment tracer la trajectoire d'un point d'un cercle qui roule sans glisser sur une droite ? Peut-on la comparer à une ellipse ? Peut-on la définir "paramétriquement" ? Peut-on calculer l'aire située sous une arche de cette courbe ?

Écoles primaires en Maine et Loire : écoles Jean-Jacques Rousseau et Charles Bénier (Angers). Écoles Jacques Prévert (Saumur) et du Dolmen (Bagneux)

Projet en classe entières (cycle 3). Contact : Jean Mainguené; Chercheur Pierre Duchet et Jean Mainguené

Le pigeon voyageur

Où un pigeon voyageur effectuant trois aller-retours par semaine dans trois villes différentes doit-il installer son nid pour se fatiguer le moins possible ?

Cartes à plier

Comment plier une carte (pour la première fois) ? Observez et reproduisez les pliages de diverses cartes du commerce : comment faire ? Y a -t-il des pliages plus commodes que d'autres ? Lesquels ? Pourquoi ? Comment faire pour refermer une carte ouverte en respectant la forme des plis (vallées : ou collines : ) ? Y a-t-il plusieurs manières de faire ? Inventez vos propres pliages, posez-vous des questions et discutez-en.

Dominos et damiers

Il s'agit de couvrir exactement, de paver, des damiers ou des morceaux de damiers avec des dominos.

Les triplets de Pythagore

Collège Robespierre (Épinay), Collège Elsa Triolet et Lycée Paul Eluard (Saint-Denis)

Contacts : A. Bourbouze, Adrien Fryc, Alain Huet. Chercheur : François Parreau

Sujet 1 - Les Tours sur l'échiquier à trois dimensions

Le problème bien connu des dames de l'échiquier consiste à trouver combien de dames au minimum faut-il placer sur un échiquier pour qu'ensemble elles contrôlent toutes les cases. Si on remplace les dames par des tours, le problème est plus simple, mais en dimension 3 ?

L'échiquier à trois dimensions est un cube partagé en nxnxn cases, chacun des côtés étant divisé en n intervalles égaux. Une "tour" contrôle les trois lignes de cases parallèles aux côtés passant par la case où elle se trouve. On se demande combien au minimum placer de tours, et comment peut-on les placer, de façon qu'elles contrôlent tout l'échiquier (commencez avec n = 2, 3, 4,...).

Sujet 2 - Les décimales des fractions

Vous savez sans doute que lorsque on calcule les décimales successives d'une fraction on obtient toujours un bloc qui se répète indéfiniment, autrement dit que la suite des décimales est périodique à partir d'un certain rang. Vous savez peut-être que, réciproquement, toute suite de décimales périodique correspond à un nombre fractionnaire. Au delà de ce résultat que vous pourrez commencer par démontrer, on peut remarquer des propriétés curieuses (regardez par exemple les décimales de 1/7) et se poser beaucoup de question :

" Si on change le numérateur de la fraction en gardant le même dénominateur, trouve-t-on toujours la même période ? le même bloc de décimales répété ? Que peut-on dire des décimales de 1/n ?

"Quelles sont les fractions correspondant aux suites de décimales de période 2, 3, 4 ? Pouvez-vous résoudre le puzzle :

Comme c'est en anglais, la virgule est remplacée par un point et on n'a pas écrit le 0 avant. Il s'agit de remplacer chaque lettre par un chiffre, deux lettres différentes correspondent à des chiffres différents et on demande en plus que la fraction soit irréductible.

Sujet 3 - Trajectoires dans le billard rectangulaire

Dans les billards mathématiques, les boules n'ont pas d'épaisseur et il n'y a ni effet ni frottement : on étudie la trajectoire d'un point qui se déplace en ligne droite à l'intérieur d'un rectangle et rebondit sur les côtés avec la seule règle "angle de réflexion = angle d'incidence"

On peut aussi considérer qu'il s'agit de la trajectoire d'un rayon lumineux qui se réfléchit les côtés comme sur des miroirs (et utiliser les symétries pour la construction géométrique).

Une trajectoire est déterminée par un point de départ (sur un côté) et une direction initiale. On se demande si, avec ces données, on peut trouver dans quel ordre 1es côtés seront touchés.

On propose de coder "0" lorsque la trajectoire touche un côté horizontal et "1" lorsqu'elle touche un côté vertical : une trajectoire correspond donc a une suite de "0" et de "1". Étant donnés un point de départ sur un côté et la pente initiale de la trajectoire, comment déterminer cette suite?

Vous pourrez vous ramener au cas d'un carré et étudier d'abord les cas où la trajectoire revient sur elle-même et continue de façon périodique, en commençant par les plus petites périodes.

Sujet 4 - Distances de la Lune et du Soleil

Ces distances ont été évaluées dès l'Antiquité par Aristarque, peu après qu'Érathostène ait réalisé une mesure du rayon de la terre. Bien sûr les résultats étaient très approximatifs, surtout pour le Soleil, mais il a fallu attendre les progrès de l'astronomie XVII-ème siècle pour trouver mieux et, comme disent les Cahiers Clairaut, "Il peut être cependant instructif de revenir sur les mesures anciennes : elles étaient fondées sur des principes simples qui restent à la base des mesures modernes..."

Pouvez-vous imaginer comment un observateur attentif, sans instrument de grande précision, avec un modèle simplifié du système solaire et une bonne intuition géométrique, peut se faire une idée assez précise de la distance de la Lune puis de celle du Soleil ?

Lycées Romain Rolland de Goussainville et Georges Braque d'Argenteuil

Atelier scientifique. Contact : J. Durlewanger ; Chercheur : Stéphane Labbé

Sujet 1 - Focalisation de la lumière.

Étudier en 2 dimension les miroirs d'équation : ax² + by² +cxy + dx + ey + f = 0, en supposant que la source parte d'un point donné, lieu de focalisation.

Sujet 2 - Galerie d'art.

Combien faut-il de gardiens au minimum pour surveiller une salle de musée polygonale. Que se passe-il si l'on rajoute des obstacles ?

Sujet 3- A l'ombre des polygones.

Existe-t-il des polygones non illuminables en tous points grâce à une source de lumière ? Envisager le cas sans réflexion sur les côtés et avec réflexion.

Sujet 4 - Enigme de Golbach.

En 1742, Goldbach envoya une lettre à Euler pour lui poser la question : " Tous les entiers > 5 sont-ils somme de 3 nombres premiers ?" Alors Euler formula une autre question : "Tous les entiers pairs différents de 4 sont-ils somme de deux nombres premiers ?" .

Sujet 5 : Le verger aveuglant.

Un verger, de forme circulaire, est composé d'arbres plantés aux intersections d'un quadrillage régulier. Le centre du verger est un noeud du quadrillage (où il manque un arbre). Quelles sont les hypothèses à faire (sur le rayon du verger, le diamètre et la distance des arbres), pour qu'il soit impossible à un observateur, placé au centre du verger, de voir les arbres de la périphérie ?

Collèges Molière (94-Ivry) & Romain Rolland (Ivry)

Parcours différencié (classe de 5ème). Contact : Hélène Kraeutler ; Chercheur R. Mneimné

(1) Triangles sur un quadrillage.

Dénombrement des triangles ayant pour sommet des noeuds d'un quadrillage donné.

(2) Pile ou face.

Quelles stratégies dans un jeu de pile ou face contre une banque ?

Lycée Jean Macé de Vitry

Atelier Scientifique. Contact : Karine Van Effenterre ; Chercheur : Christophe Hazard

Le Hasard.

Qu'est ce que le hasard ? Les décimales de sont telles distribuées au hasard ?

Collèges Frédéric Chopin et école élémentaire Jules Ferry de Melun

Atelier scientifique. Contact : Ludovic Moreau ; Chercheurs : Olivier Bodini et Pierre Duchet

Sujet 1 : Alphaville

A Alphaville, les rues forment un quadrillage rectangulaire. Les habitations sont ainsi divisées en "blocs". Nous voulons équiper Alphaville en installant des cabines téléphoniques à certains carrefours; nous voulons que chaque carrefour de la ville soit situé à au plus n blocs d'un téléphone. Suivant les dimensions d'Alphaville et la valeur du nombre n trouver des solutions avec le moins de stations possibles.

Sujet 2 : Aux antipodes l'un de l'autre

Des astronautes escargots sont sur une boite à chaussure, perdus au plein milieu de l'espace. Ils se rejettent la responsabilité de l'erreur qui les a mis dans une telle situation. Depuis, ils se font la tête au point de chercher à se placer sur cette boite de manière à être le plus éloigné possible l'un de l'autre. Où peuvent-ils se mettre ?

Sujet 3 : Le jeu d'Alésia

Un terrain est formé de cases alignées avec une case centrale, contenant un bouchon, séparant le terrain en deux camps de même longueur. Chacun des deux joueurs dispose d'une réserve de N jetons. A chaque tour de jeu, les joueurs prélèvent secrètement dans leur réserve un certain nombre de jetons puis comparent leur nombre. Celui qui a choisi le nombre le plus élevé pousse le bouchon d'une case vers son adversaire, les jetons utilisés sont retirés du jeu. En cas d'égalité les jetons sont alors remis dans la réserve et on rejoue le coup. pour gagner, il faut réussir à pousser le bouchon dans la dernière case du camp adverse. Quand les deux réserves sont vides sans que le bouchon soit arrivé au bout, la partie est nulle. Y a-t-il des stratégies meilleures que les autres ? Inventez une machine qui joue le mieux possible. Pourra-t-elle battre votre chercheur ? Modifiez à votre guise la longueur du terrain et le nombre de jetons. Est-ce plus facile avec moins de cases, moins de jetons ?

Collèges Robespierre (Epinay sur Seine) et Elsa Triolet (Saint Denis)

Contact : J. Bourbouze et Adrien Fryc ; Chercheur  : Benoît Rittaud

Sujet 1 : Sauts de puce sur un cercle

Le cercle C de centre O est le terrain de sport d'une puce qui s'y déplace par bonds. La vigueur des sauts est toujours la même, c'est-à-dire que, Si la puce se trouve en A, alors le saut l'amène au point B tel que l'angle AOB soit égal à une valeur a fixée. Une fois la puce en B, elle saute de nouveau pour atteindre le point C tel que l'angle BOC = a, et ainsi de suite (la puce saute toujours dans le Sens inverse des aiguilles d'une montre). Cette situation permet de se poser plusieurs questions:

- Partie d'un point initial, la puce reviendra-t-elle, au bout d'un temps plus ou moins long, à ce point initial? Ou à un point quelconque qu'elle a déjà visité ? Comment trancher à partir de la valeur de a?

- Si la puce ne revient jamais à son point de départ, visitera-t-elle tous les points du cercle ? Y aura-t-il des arcs de cercle à l'intérieur desquels elle n'ira jamais? Ou au contraire, des arcs de cercle dans laquelle elle ira particulièrement souvent? - Si la puce revient à son point de départ, combien de points la trajectoire contient-elle? Plusieurs valeurs différentes de a peuvent-elles donner le même ensemble de points visités par la puce ? Et dans ce cas, qu'est-ce qui change? Comment?

Sujet 2 : Trajectoires sur un écran.

On considère un écran d'ordinateur, représenté par un quadrillage de forme rectangulaire, ayant a carrés (ou "pixels") en longueur et b carrés en largeur. On noircit l'un des carrés de l'écran, qui donne la position d'une balle, puis le carré situé immédiatement au-dessus et à droite, et ainsi de suite en suivant la même direction, jusqu'à cogner l'un des bords de l'écran, lequel fait rebondir la balle: Si, par exemple, on est amené à cogner le côté supérieur de l'écran en venant de la gauche, alors le carré noirci suivant sera celui qui est immédiatement en bas et à droite du précédent. (on comprend ça très bien avec un dessin). Dans les cas particuliers où l'on atteint 1'un des 4 coins de l'écran, on considère que la balle rebrousse chemin, en suivant la même trajectoire. mais à l'envers, Les trajectoires sont-elles toujours périodiques, autrement dit, une fois la balle partie, revient-elle toujours sur ses propres traces avec un parcours identique ? Peut-on trouver une trajectoire qui passe par tous les "pixels" de l'écran? Sinon, de combien de trajectoires a-t-on besoin pour effectuer un recouvrement de l'écran, en fonction de a et de b? Y a-t-il toujours des trajectoires avec boucles? Sans boucle ? Combien de trajectoires n'atteignent aucun des 4 coins de l'écran ? On peut aussi se poser ces questions pour des écrans de forme plus compliquée (en L, en U etc.)

Sujet 3 : Empilement de sphères

On se donne une quantité indéfinie de sphères rigides de même rayon, et on se demande comment les disposer pour que, ensemble, elles prennent le moins de place possible. Comment faire? Comment savoir si une disposition est plus économe en place qu'une autre ? Y a-t-il plusieurs dispositions équivalentes? Dans un premier temps, on pourra se poser ces questions dans le plan, avec des disques de même rayon. On pourra aussi chercher dans des livres quelques exemples de cristaux dont l'arrangement spatial des atomes correspond à ceux qui auront été trouvé.

Collège Molière (94-Ivry sur Seine)

Parcours différencié (classe de 5ème). Contact : Hélène Kraeutler ; Chercheur : Mneimné ?

sujet 1 : Le "QCM"

Un "QCM" comporte 20 questions, 4 choix par question, une seule bonne réponse par question.

Comment le professeur doit-il noter pour que les élèves n'aient pas intérêt à répondre au hasard à une question quand ils ne connaissent pas la réponse ?

Sujet 2 : Le trésor

Un trésor est placé au centre d'une enceinte comportant 7 chemin horizontaux et 7 chemin verticaux. Une personne est déposée au hasard à un carrefour de cette enceinte et a 60 minutes pour trouver le trésor. Sa visibilité est restreinte au carrefour suivant, elle ne se souvient que du "dernier" tronçon qu'elle a parcouru et met 10 minutes pour parcourir un tronçon. Est-il intéressant de participer à ce jeu ?

Collèges République (93 Bobigny, ZEP) et Langevin (93 Drancy, ZEP en 1999-00)

Ateliers scientifiques jumelés avec le collège Camille Sée (Paris) . "Recherche mathématiques"

Contacts : Christelle Hourné, Soraya Terbèche ; Chercheur Olivier Bodini.

(Photos du congrès 2000)

Sujet 1 : Escargots sur un cube.

Des escargots sur un cube se détestent. Où peuvent-ils se mettre de manière à être le plus éloigné possible l'un de l'autre ?

Sujet 2 : Communication sur une grille.

Des personnes (ou des relais électroniques, si vous préférez) sont régulièrement disposées dans un plan, aux noeuds d'un quadrillage infini. Chaque personne peut envoyer des informations à d'autres personnes, à condition de respecter certaines règles. Ces règles, bien précises et immuables, sont les mêmes pour toutes les personnes. En fait, à proprement parler, c'est l'ensemble de ces règles qui définit le "réseau".

Exemple de réseau : trois règles appelées A, B, C.

règle A: on transmet à la personne située 3 pas vers l'est et 2 pas vers le nord.

règle B: on transmet à la personne située 2 pas vers l'ouest et 1 pas vers le nord.

règle C: on transmet à la personne située 1 pas vers l'est et 3 pas vers le sud.

Les règles de transmission d'un réseau étant fixées, le problème est le suivant : une nouvelle, connue d'une personne particulière peut-elle être transmise à tout le monde en suivant les règles du réseau ? Sinon, quelles sont les personnes qui peuvent être informées ? Le problème général, non résolu à ce jour, peut être abordé sous bien des aspects :

* Si chacun diffuse immédiatement ce qu'il sait en utilisant toutes les règles, comment se propagent les nouvelles ? En particulier, on peut se demander combien de personnes seront au courant au bout de 1,2, 3,..., n étapes.

* Comment savoir Si une personne choisie à l'avance pourra être informée ? En combien d'étapes? De quelle manière?

* Si on ne trouve aucun moyen de prévenir quelqu'un, comment être vraiment sûr qu'il n'existe aucun moyen?

* Y a-t-il des réseaux plus efficaces que d'autres pour la diffusion ?

Pour des dispositions moins régulières des personnes à prévenir, peut-on trouver des méthodes de diffusion rapides générales?

Sujet 3 : La période trouble des inverses.

Regardons ensemble les nombres 1/2 ; 1/3 ; 1/4 ; 1/5 ; 1/6 ; 1/7... Leur écriture décimale est 0,5 ; 0,3333... ; 0,25 ; 0,2 ; 0,16666... ; 0,142857142857.... On remarque deux choses, soit l'écriture décimale est finie comme pour 1/2, 1/4, 1/5, soit il semble qu'à partir d'un certain stade, il y a un groupe de chiffre qui se répète indéfiniment, c'est la période du nombre. Par exemple, pour 1/3, c'est 3 ; pour 1/6, c'est 6 ; pour 1/7, c'est 142857.

On appellera longueur du nombre n le nombre de chiffres que contient la période de la fraction 1/n. Quand l'écriture de 1/n est finie, on dira que la longueur de n est 0. (Le tableau des longueurs des nombres entiers de 1 à 20 figure sur le texte du sujet)

Problème : existe-t-il des nombres de longueur 1999 ? Plus généralement étant donné un nombre N, peut-on trouver un nombre dont la longueur est N ?

Peut-on caractériser (trouver des propriétés) les nombres de longueur 0 ? 1 ? etc... Les nombres 7, 17, 19 ont des longueurs de 6, 16, 18. Existe-il d' autres nombres N dont la longueur est N-1 ?

Sujet 4 : Le bon pli

Comment plier un triangle de telle façon que l'aire du polygone obtenu soit la plus petite possible ? (On ne fait qu'un seul pli et le polygone considéré est le plus grand possible, vu après ce pliage).

Lycée Romain Rolland de Goussainville et Lycée Georges Braque (Argenteuil)

Atelier scientifique. Contact J. Durlewanger ; Chercheur : Stéphane Labbé

Le problème des fous

Sur un échiquier combien de fous peut-on placer au maximum sans qu'ils puissent se détruire les uns les autres ?

Lycée Jean "Macé" de "Vitry (établissement sensible, classé PEP 1)

Atelier scientifique. "Questions Scientifiques: Controverses et polémiques"

Contacts: Jean Carroy & Karin van Effenterre . Chercheur : Christophe Hazard

voir photos

Thème 1 : le son du "steel"-"drum"

Fabrication de l'instrument, analyse des sons, définition des notes. (photo de l'atelier au congrès 2000)

Thème 2 : l'évolution:

Peut-on prévoir l'homme du futur ? que donnent certaines lois simples d'évolution de populations ?

Thème 3 : la santé des jeunes:

Qu'en disent les médias ? Que peut on en savoir ?

Lycée Louise-Michel (93-Bobigny) et mjc Daniel André (Drancy).

Atelier scientifique . "Géométries exotiques"

Contact et animateur : François Gaudel ; Chercheur : Pierre Duchet

(Voir photos)

Thème d'activité : les géométries finies.

Géométries avec un nombre fini de points et de droites. Exploration, visualisation et matérialisation de plans affines et projectifs, avec baguettes, ficelles colorées et logiciel de dessin vectoriel. Réalisation d'un exposition et d'une communication.

Lycées Louise Michel (93-Bobigny) et Jean Jaurès (94-Montreuil)

Atelier scientifique. "Faire des maths autrement"

Contact : Jean-Denis Brulois, Chercheur: Virginie Lasserre

(Participation au congrès 2000)

Thème d'activité : à quoi servent les fonctions ?

Sur la dynamique des populations. Une expérience de sondage (taille/poids). Sur la construction de la coquille de l'escargot. Sur une méthode numérique pour trouver un minimum. Ces quatre sujets ont un point commun : le nombre d'or et la suite de Fibonacci.

© MATh.en.JEANS 2000. Tous droits réservés.