.

Ateliers "MATh.en.JEANS" de recherche dans la classe.

Ateliers de recherche sur 12 semaines, Expérience pilote de l'Académie des pays de la Loire, décembre 1997- mars 1998.

Écoliers ayant indiqué leur participation

Couleurs de Guthrie : Jérome, Alexis, Bruno ; Sandrine Chevé, Marie-Laure Cormier, Jérémy Dubois et Jérémy Laborie ; Sylvain Chaniau, Jérémy Franqueville, David Oliveira, Julien Rabouan.

Les balances de Jullien : Sandrine Chevé, Marie-Laure Cormier, Jérémy Dubois et Jérémy Laborie,

Le cavalier d'Euler : Alexandre T., Manuel B.

Les pentaminos : Aurélia, Allison, Jérémy, Marina, Nora, Sonia, Sabrina, Vanessa,

Les tresses d'Artin : Yohan Mercier, Emeline Perdriau, Justine Lalik, Mohamed Sdiri.

Les satellites : Julie F., Alexandra N., Pauline L., Caroline B., Florent N., Yohan Mercier, Emmanuel C., Sandra S.

Enseignants : Mme Leborgne et M. Richard (Saumur), M. X et M. Y (Angers)

Chercheurs : Pierre Duchet (Combinatoire, UPR 175 du CNRS, Paris), et J. Mainguené (Calcul formel, IUFM des pays de la Loire, Angers).

---

[ Article vérifié et commenté. Les textes entre crochets sont des éditeurs. Notes, commentaires et annexes sont placées en fin d'article.]
[Sauf précision contraire, les passages entre guillemets sont des citations des manuscrits des écoliers.]

(échos de la presse régionale)

"SAUMUR. Deux classes jouent aux maths avec un chercheur du CNRS"

(encadré 1ère page de "La Nouvelle République du Centre-Ouest", 7-8 mars 1998).

"math.en.jeans, la recherche en s'amusant" (Titre de l'article, Ibid., page 3)

ANGERS "Les maths de demain" ..." Les potaches planchent sur les maths de demain" (encadré 1ère page et titre de l'article en pages intérieure dans "Le Courrier de l'Ouest", Samedi 7 mars 1998)

(1) Les couleurs de Guthrie. Le problème du coloriage d'une carte de géographie avec le moins de couleurs possible : les pays frontaliers doivent être de couleurs différentes.

(2) Les balances de Jullien. Peser des nombres pour les écrire : inventer son propre système de numération.

(3) Le cavalier d'Euler : Problème ancien du voyageur de commerce moderne : passer dans le plus d'endroits possible sans repasser deux fois au même endroit.

(4) Des pions et des lignes. Un pion suffit à surveiller les lignes qui le contiennent. Combien de pions-gardiens suffisent pour surveiller toutes les lignes ? Les satellites sont une variante du problème précédent, étudiée par certains écoliers : un pion surveille les cases voisines. Combien de pions-gardiens suffisent pour surveiller toutes les cases ?

(5) Les tresses d'Artin. Comment dénouer une tresse par addition d'une autre tresse ?

(6) Les pentaminos paveurs. Avec des morceaux d'échiquier comportant 5 cases, comment fabriquer un carreau de forme compacte ?

La structure est celle du dispositif Math.en.Jeans classique : un jumelage entre deux classes d'établissement différents ; des "séminaires" permettent la mise en commun et les discussions entre les deux groupes qui étudient le même sujet.

Écolier(e)s discutent entre eux, par groupe, échangent avec leur instituteur, en parlent à leur parents...Ils (elles) apprennent peu à peu à comprendre et à expliquer leur sujet, leurs pistes d'exploration, leurs résultats, leurs démarches. Avec l'aide de leur maîtres et de discussions avec le chercheur, ils orientent et structurent leur travail et prennent conscience de manières rigoureuses de s'exprimer ainsi que des méthodes qu'ils ont eux-mêmes choisies...

Calendrier suivi en 1997-98.

Séminaire 0 (5 décembre). Présentation des sujets et de l'activité.

3 séances. Choix des sujets. Phase de découverte et d'exploration. Formulation de questions.

Séminaire 1 (23 janvier). Echange des informations. Passage à la formulation et à l'expérimentation

2 séances. Formulation de projets (hypothèses) et expérimentation. Mise en évidence de résultats

Séminaire 2 (6 mars). Préparation du congrès : discussion des résultats; passage à l'argumentation.

2 séances. Formulation de lois. Argumentation. Vérification. Préparation de l'exposé.

Congrès (27 mars). Exposés, posters et discussions. Evaluation, mise en corrélation des lois.

1 séance. Synthèse écrite des lois et des arguments pour publication. Bilan et "institutionnalisation".

(fiche fournie aux écoliers et accompagnant la présentation orale du sujet.)

On veut colorier une carte en employant le plus petit nombre de couleurs possible, avec les règles suivantes :

On peut commencer avec une "carte" qui ressemble à un mur de briques irrégulières.

• Essaie de la colorier avec 7 couleurs différentes, puis avec moins si c'est possible.
• Peut-on imaginer une règle générale pour colorier un mur de briques quelconque ?
• Après on travaille avec la carte de l'Afrique, puis avec des cartes de ton invention.

Les briques

Ceci est interdit : . Mais ceci est permis .

Coloriage par la règle : "il faut commencer par la première ligne puis par la deuxième, etc."

Cette "règle" fonctionne en fait en colorant avec la première couleur possible ; elle exprime ce que les informaticiens appelle l'algorithme glouton :

• on colore successivement les pays, dans un ordre quelconque que l'on fixe d'abord, une fois pour toute.

• on n'utilise une nouvelle couleur que lorsque c'est indispensable

• si on peut utiliser une couleur déjà utilisée, on choisit celle qui, auparavant, a été utilisée le plus tôt.

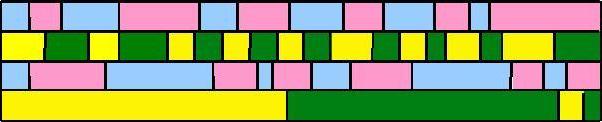
Pour le mur en briques, avec l'algorithme glouton, [en allant vers la droite, ligne par ligne], il faut 7 couleurs (Figure 4).

4 couleurs suffisent ...

"Pour colorier le mur (figure 1) nous avons utilisé 4 couleurs : on a commencé par la première ligne. Nous avons pris la première case : on l'a colorié en bleu. Nous avons pris la 2ème case : on l'a colorié en rose. Et ainsi de suite : bleu, rose, bleu, rose etc. Pour la 2ème ligne, nous avons pris deux autres couleurs. Nous avons colorié la 1ère case en jaune et la 2ème en Vert. Et ainsi de suite : jaune-vert-jaune-vert etc. Après on a colorié la 3ème ligne : bleu-rose-bleu-rose etc. Et la 4ème ligne jaune-vert-jaune etc."

Plus généralement ?

Divers essais ont été faits diverses cartes : l'Afrique, l'Europe, la France des départements, des cartes où les pays sont des rectangles ou des réunions de rectangles contigus, ou encore ont une forme géométriques (exemple avec 65 pays sur la figure 6) : après des tentatives avec un petit nombre de pays (3, 4, 5,..., 16, et même ), ou avec un petit nombre de couleurs (2, puis 3, puis 4, ) après des coloriages réussis avec 7 couleurs, après des discussions et des améliorations successives, il y a eu dans chaque cas un groupe d'élève qui a finalement trouvé que 4 couleurs suffisaient. [1]

Le fait que le nombre de couleurs n'augmente pas avec le nombre de pays a quelque peu surpris les enfants.

Parmi ces cartes, celles de l'Afrique et de la France des départements ont été les plus difficiles à colorier. L'idée de changer l'ordre de coloriage a été finalement celle qui a réussi : un chemin "de la Bretagne aux Pyrénées" pour la France ; pour l'Afrique..."on commence par la fin"

Il a semblé impossible de faire mieux (colorier en 3 couleurs) pour les cartes de l'Afrique et de la France : qu'en pensez-vous ?

Le sujet

(fiche fournie aux écoliers et accompagnant la présentation orale du sujet.)

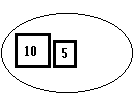
Le mathématicien Pierre Jullien (IUFM d'Aix-Marseille) propose d'écrire les nombres avec des balances. On place un poids N sur le plateau de gauche et, en utilisant un système de poids connus, par exemple 1,2,5,10, on réalise un équilibre :

	Exemple     Avec le système 1,2,5,10
	le nombre 3 peut être pesé de plusieurs manières

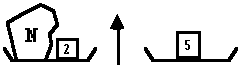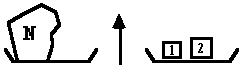D signifie dans le plateau de droite G signifie dans le plateau de gauche O signifie hors de la balance Pour écrire le nombre on réalise une pesée du nombre. on écrit la position de chaque poids	En pratique, on réserve une colonne pour chaque poids (du plus petit à droite au plus grand à gauche)   Et on écrit la position du poids (G, D ou O) dans la colonne correspondante			10	5	2	1
Dans le système 1,2,5,10 , le nombre 3 s'écrit (première pesée)				O	D	G	O
ou (deuxième pesée)				O	O	D	D

Pour éviter d'avoir plusieurs écritures pour un même nombre, on peut choisir une façon particulière de peser. Notre écriture décimale en est un exemple :

Figure 8

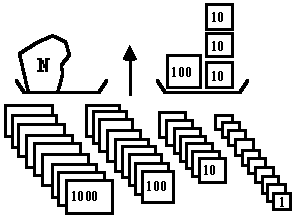Les poids utilisés sont 1, 10, 100, 1000, ...(etc.) chacun en neuf exemplaires On décide de les mettre toujours à droite. Pour chaque type de poids de base, on écrit un seul chiffre, qui indique le nombre de D nécessaires Ici on a écrit "cent trente":

1000                 0

100                 1

10                 3

1                 0

 
• Inventez votre propre système balançaire et réalisez des additions, des soustractions etc..... Jullien propose de prendre des poids 1,3, 9 pour commencer...

Motivation. Les ordinateurs utilisent volontiers les poids 1,2,4,8,16, ...: c'est le "système binaire".

Des maisons, des hôtels, et des plombs

Comment se constituer un matériel permettant de faire les expériences ? Hôtels et maisons du jeu de Monopoly® ne conviennent pas bien car un hôtel ne pèse pas exactement un nombre entier de maisons ! Un ajustement avec des morceaux de pâtes à modeler n'est pas commode...

Primus, Secondus, ...

"Nous avons créé notre système numérique" ...Il s'appelle BJu-JJR.

Il y a "des unités du premier, du deuxième et du troisième degré" réalisées avec "1 hôtel, 2 hôtels attachés ou 3 hôtels attachés"

Il y a ensuite des unités appelées "primus, secondus, tertius, quartus et quintus", réalisées respectivement avec 1,2,3,4 et 5 plombs attachés ensemble.

"Un hôtel vaut de plomb [...] Nous n'avons pas choisi les maisons du monopoly car elles n'étaient pas exactement la moitié d'un hôtel".

Un exercice d'écriture

"Complétez grâce à l'exemple" :

Système BJu-JJR	écriture exemple	écriture pesée n°1	écriture pesée n°2
Primus Secondus Tertius Quartus Quintus	D - 1 0 0 D - 1 G - 2 D -1	... ... ... ... ...	... ... ... ... ...	exemple
1er degré 2ème degré 3ème degré	0 0 0	... ... ...	... ... ...	pesée n°1
				pesée n°2

[Pour d'autres documents sur ce sujet -NDLR]

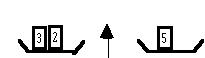"Le cavalier d'Euler est un problème de mathématiques qui consiste à déplacer un cavalier dans un échiquier sans passer plusieurs fois sur la même case. Il faut essayer de remplir le plus de cases possibles."

Le sujet

(fiche fournie aux écoliers et accompagnant la présentation orale du sujet.)

" Le cavalier d'Euler "

Sur un échiquier un cavalier se déplace en parcourant deux cases tout droit et une case de coté.

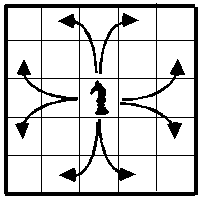
• Sur combien de cases au maximum, peut aller un cavalier, sans passer deux fois sur la même ?

• Sur un échiquier 5x5 : en partant du centre ? En partant d'une autre case ?

• Sur des échiquiers plus grands: 6x6, 7x7, 8x8 (l'échiquier normal) ?

• Peut-il aller sur toutes les cases ?

Traceurs ou sauteurs ?

[Les appellations de cette section sont les miennes (P.D.) ; elles seront utilisées dans la suite]

Il est remarquable de voir à quel points les écoliers ont voulu préciser les règles. Les déplacements de cavalier qu'ils effectuent sont très souvent des trajectoires tracées sur le papier, parfois même de véritables chemins formés avec les cases traversées. Au début de leur activité, beaucoup ont choisi d'interdire la traversée des tracés ou des cases déjà parcourues.

Ainsi, des discussions très animées ont égayé le "premier séminaire" (voir plus haut la section intitulée "La forme de l'expérience pilote"): les records des uns et des autres dépendaient des règles adoptées qui n'étaient pas les mêmes pour tous.

Voici les principales espèces considérées.

1. Les cavaliers traceurs d'Attila

Les cavaliers traceurs marquent leur parcours sur l'échiquier, au fur et à mesure qu'ils avancent et, comme les redoutables cavaliers d'Attila, il détruisent définitivement l'herbe sur leur passage : un cavalier ne peut ni toucher ni croiser le chemin déjà tracé.

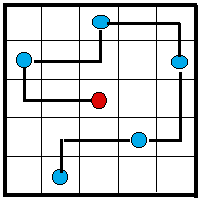
1a. Le cavalier-équerre Le cavalier d'Attila présenté par cette figure est un "cavalier-équerre" : chaque déplacement se fait en avançant d'abord de deux cases dans un sens puis d'une case vers la droite ou la gauche. Les cases traversées sont interdites pour la suite du parcours.   Dans un 55, il semble qu'un cavalier-équerre ne puisse pas faire plus de 5 étapes en partant du centre (voir figure 12).	Figure 12
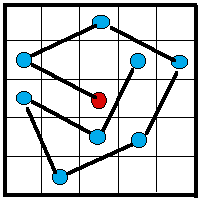
1b. Le cavalier diagonal   Partant du centre, un "cavalier diagonal " d'Attila peut être bloqué après 9 étapes sur un 55 (figure 13).     En s'y prenant autrement, peut-on réussir à faire plus d'étapes ?	Figure 13
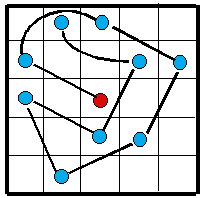
Partant du centre, un cavalier d'Attila peut faire 10 étapes sur un 55.   On remarque qu'il peut revenir à son point de départ .   La aussi se pose la question :   peut-on faire mieux ?	Figure 14

2. Les cavaliers sauteurs

Au "deuxième séminaire" (voir plus haut la section intitulée "La forme de l'expérience pilote"), beaucoup avaient adopté la règle la moins contraignante, qui permet au cavalier de sauter sans laisser de traces... Pour les cavaliers sauteurs, seules les cases sur lesquelles ils s'arrêtent sont interdites pour la suite du parcours.

Pour communiquer, on numérote...

"Nous avons travaillé à deux pour voir le fonctionnement et chercher des solutions de déplacements sur les différents échiquiers. Puis, quand on pensait trouver une règle [un moyen de réussir un bon parcours-NDLR] on la communiquait à l'autre camarade pour voir si c'était possible" [c'est à dire pour voir si la "règle" était efficace-NDLR].

Pour décrire les parcours, les écoliers ont numéroté dans l'ordre les cases successivement atteintes par leur cavalier sauteur, le numéro 1 étant attribué à la case de départ.

Dans cet exemple (figure 15), une espèce particulière de "cavalier traceur" a sans doute été choisie. Malheureusement la règle des déplacements autorisés ne nous est pas parvenue...   "Le meilleur échiquier que l'on a fait est un 88: on a rempli 20 cases; jamais le cavalier n'est passé deux fois sur une case déjà remplie".

Figure 15

Qui dit mieux ?

Des records ont été établis, puis battus. Plusieurs observations ont été faites, certaines conduisant à des "lois" [des résultats, ou des phrases, qui sont vraies par expérience et sur lesquelles tout le monde se met d'accord]. Diverses "techniques" générales ont été proposées, par exemple: "pour les quadrillages plus grands, on utilise la technique de la spirale" où "le déplacement se fait en "escargot"...".

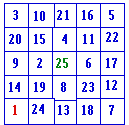
Ci-dessous des extraits des résultats obtenus; à vous de repérer les techniques qui ont été utilisées! [Les couleurs sont placées par l'auteur de l'article].

Loi 1. "Cet échiquier ne peut se remplir complètement."	Loi 2. "Cet échiquier ne peut se remplir complètement."
Loi 3 "C'est gagné, on peut remplir complètement cet échiquier"	Loi 4 "On peut faire le chemin inverse."

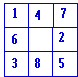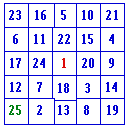Escargots et partitions

Des parcours méthodiques.

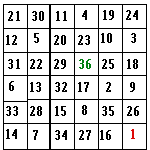
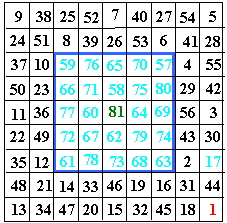
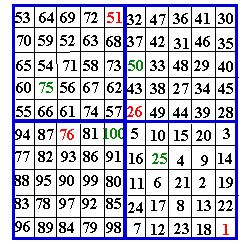
A suivre...

_____________

NOTES

[1] Francis Guthrie a suggéré que 4 couleurs suffisent pour n'importe quelle carte.