Echos de la recherche 3A 05.02

Contribution de Charles Payan (CNRS, Grenoble)

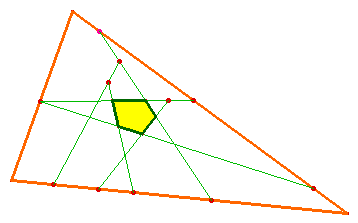
[Plus généralement, étant donné un triangle.]

On place des pts n'importe où, sur les cotés, sur les segments induits par ces pts ...etc ; on considère n'importe quel polygone  induit par des droites engendrées par ces pts : le rapport des aires entre triangle et polygone ne dépend que das rapports correspondants aux pts placés.

[Preuve]

- Evident sur le(s) triangle équilatéral puisque ces rapports sont les seuls paramètres de la figure..
- Tout triangle est la projection sur un plan parallèle d'un triangle équilatéral
- la projection parallèle conserve les rapports de longueur et d'aire.

Question : comment montre-t-on que la projection parallèle est la seule transformation qui conserve les rapports de longueur et d'aire ?