Sujet : Pavages : carrelages sur un réseau triangulaire. [poster]
nb d'élèves : 4 & 3+3

"Carreler" une surface (ou, comme disent les mathématiciens, "paver" cette surface), c'est la couvrir exactement,avec des "carreaux" (les "pavés"), sans chevauchement, ni interstice.

Les cases d'un réseau triangulaire sont des triangles équilatéraux égaux. Une forme constituée de plusieurs cases assemblées s'appele un "polyamant". Avec plusieurs "carreaux", tous égaux à un polyamant donné pris comme modèle, on cherche à "carreler" des surfaces de formes diverses.

• Possible ou impossible ? Comment décider ?
• Si c'est possible, comment ?
• Peut-on poser le premier carreau n'importe-où ?
• Si c'est impossible, comment en être sûr ?

On peut tester les polygones les plus simples (triangles, quadrilatères, pentagones, hexagones, etc.) aussi bien que les formes quelconques, en particuliers les surfaces parsemés d'obstacles ("trous").

Ci-dessous quelques entrées possibles dans l'univers des polyamants.

1. Les diamants (forme losange)	"Le losange est un carré italique, une figure du costume d'Arlequin, une figure souple comme les sonorités de son nom."                                              [ Geneviève Brisac ]
a. Quels hexagones sont pavables ? b. (hexagone avec un trou, figure 1) Il est impossible de paver l'hexagone de la figure 1 sans laisser une case vide. Où peut être ce trou ?

2. Les triamants (forme trapèze)
a. Quels hexagones sont pavables ? b. (hexagones avec un trou, figure 2) Il est impossible de paver l'hexagone de la figure 2 sans laisser une case vide. Où peut être ce trou ?

3. Les quadriamants longs ou dominos penchés (forme parallélogramme)
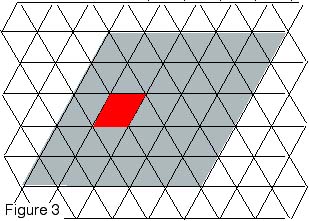
a. Quels hexagones sont pavables ? b. (Losanges avec trou, figure 3) On pose d'abord un "diamant" et on tente, avec des "dominos", de carreler le reste du losange (l'exemple de la figure a ses cotés de longueur 5 unités),. Quelles positions du diamant permettent de réussir le pavage?

Étudier les pavages, à quoi ça sert ?

Carreler une cuisine avec des carreaux identiques de forme donnée ..., est un jeu qui intéresse les mathématicien(ne)s.
Les problèmes de "pavages" ( c'est ainsi que les mathématiciens appellent les carrelages ) relève de la Combinatoire. Ils apparaissent dans des contextes aussi variés que :

- la nature
(La forme et la structure des cristaux de roche s'explique par la disposition des molécules en réseaux)

- la logique et l'informatique théorique
(le problème du pavage s'avère indécidable par ordinateur)

- la recherche pétrolière
(comment limiter le nombre de forages nécessaires à l'exploitation d'un champ pétrolifère)

- la physique des matériaux
(état à basse température des matériaux ferromagnétiques ; quasi-cristaux),

- la communication
(fabrication de codes correcteurs d'erreurs)

[Note des éditeurs] : Le même sujet est traité à Corbeil-Essonnes, . Le thème des polyamants, avec des sujets différents est également l'objet d'un atelier de méthodologie en classe de 6ème à Corbeil-Essonnes