Sujet n°1 : le problème de Steiner.

Comment relier des points par un réseau de lignes de longueur totale minimale ?

Note de la rédaction. Il s'agit du sujet 01S01 du LaboraToile , également étudié à Lomme, Lys-lès-Lannois et Villeneuve d'Ascq sous le titre "Relier des points par des segments de longueur minimale".

Sujet n°2 : Recherche de géodésiques.

Quel est le plus court chemin sur une surface pour relier un point à un autre ? Cas du cube, du pavé (parallélépipède) du cône de révolution, ...

Note de la rédaction : Sujet également étudié à Lomme, Lys-lès-Lannois et Villeneuve d'Ascq sous le titre "Recherche de chemins optimaux pour relier des points sur la surface d'un solide".

Un sujet voisin, "Aux antipodes l'un de l'autre" a été étudié les années précédentes par d'autres ateliers.

Bibliographie

Exemples de surfaces minimales, conférence de Mme Laure Quivy, (Université Paris XIII), Actes MATh.en.JEANS 1997, MATh.en.JEANS, Paris, pp. 57-60. [version pdf]

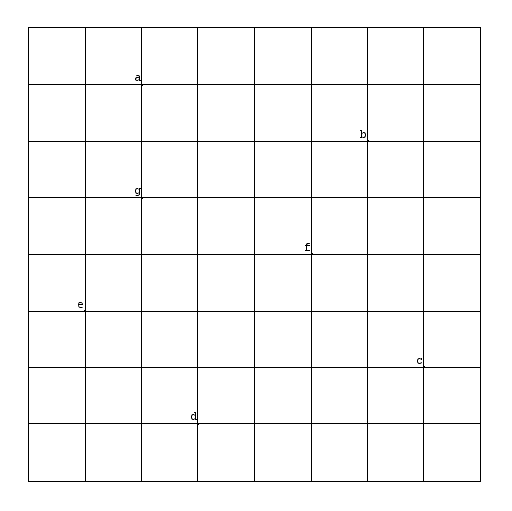
Sujet n°3 : Entourer la plus grande ou la plus petite surface possible.

Des points sont donnés parmi les noeuds d'un quadrillage (ci-dessous un exemple avec 7 points)

On cherche les polygones d'aire minimale (ou maximale) dont ces points sont les sommets.
Des questions analogues se posent aussi à propos du périmètre.

Note de la rédaction. Sujet également étudié à Lomme, Lys-lès-Lannois et Villeneuve d'Ascq sous le titre "Recherche d'une aire minimale et maximale dans un réseau de points".