|
|
|
|
|
|
M. François Thomas M. Ludovic Guichet |
|
|
|
| |
Sujet 1 : Mots complets.
On considère les mots qu'on peut écrire à partir des lettres de l'alphabet {a,b}.
Par exemple m = aabbbabab.
Un facteur d'un mot m est un autre mot, formé de lettres
consécutives de m.
Par exemple :
Le mot abba contient 9 facteurs: (le mot vide), a; b; ab; bb; ba; abb; bba; abba.
Le mot bbb n'en contient que 4: ; b; bb; bbb.
Un mot est dit complet à l'ordre k si tout mot de
longueur k apparaît comme facteur. Par exemple, le mot m (m =
aabbbabab ) est complet à l'ordre 2 (donc à l'ordre 1),
les facteurs a; b; ab; ba; aa; bb apparaissent bien. Mais ce mot
n'est pas complet à l'ordre 3, le facteur aaa
n'apparaÓt pas.
Question 1: Quelle est la longueur minimale d'un mot complet à
l'ordre k?
Question 2: Combien y a-t-il de mots complets à l'ordre k de
longueur minimale? (ex: pour k = 1 la longueur minimale = 2 mots =
{ab; ba} )
Extensions possibles : Varier la taille de l'alphabet. Mot le plus
court ayant i facteurs distincts?
Sujet 2 : Polyominos en escalier.
Un polyomino en escalier est bordé par deux chemins
formés de pas Nord et Est, n'ayant en commun que leurs
extrémitÈs.
Deux
paramËtres : Le périmètre et l'aire.
Dans l'exemple ci-contre le périmËtre est 24, et l'aire
est 15 (c'est un "P12")
Question 1: Quel est le nombre Pn de polyominos
en escalier de périmètre n ?
Question 2: Quelle est la somme an des aires de ces
polyominos ?
Question 3: En prenant ces polyominos en escalier, et en autorisant les rotations de certains d'entres eux, peut-on paver un carré?
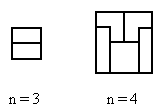
Sujet 3 : Les diagrammes aztèques. (sujet n°56 du projet "es p ace")
Un diagramme aztèque d'ordre n est un polyomino
particulier
|
|
Hauteurs des colonnes de gauche à droite 2, 4, |
Question 1: Combien de façons y a-t-il de couvrir ( ou paver) un diagramme avec des dominos qui ne se recouvrent pas?
Exemple : Un pavage de D3Question 2 : Raffiner en trouvant le nombre de pavages de Dn contenant k dominos verticaux.
