Comptes Rendus MATh.en.JEANS 98-06 

 

NB :  Cet article a été vérifié par les éditeurs. Mais, conformément au voeu de l'auteur :

Qu'est ce qu'une preuve mathématique ? On propose ici 15 situations qui instruisent le dossieret provoque le débat. Quelques repères et références seront utiles aux lecteurs exigeants et aux enseignants.

Théorème 1. Dans le plan euclidien, les médianes d'un triangle sont concourantes .

Preuve A. On réalise avec le logiciel Cabri-Géomètre^© la construction des médianes d'un triangle de base. La vérification par le logiciel de la propriété "concourance" donne le message "ces droites sont concourantes dans le cas général ". CQFD

Preuve B. A partir des propriétés des parallélogrammes, du "théorème des milieux" et des propriétés des longueurs, et des définitions des nombres, on établit d'abord les lemmes suivants.

(1) Un triangle quelconque et son triangle des milieux ont mêmes médianes.

(2) Les points de concours des médianes d'un triangle sont intérieurs au triangle des milieux.

(3) les longueurs respectives des côtés du triangle des milieux sont moitié de celles du triangle.

(4) La distance de deux points intérieurs à un triangle ne dépasse pas la longueur du plus long côté.

(5) Si a et b sont deux nombres positifs, en divisant a par 2, puis le nombre obtenu par 2, puis encore par 2, etc., on aboutit toujours à un nombre inférieur à b.

Faisons l'hypothèse (H) : Il existe un triangle T dont les médianes ne sont pas concourantes. Les médianes d'un tel triangle forment un triangle Q dont la longueur du plus grand côté est notée t.

Soit T1 le triangle formé par les milieux des côtés du triangle T, T2 le triangle formé par les milieux des côtés du triangle T1, et ainsi de suite... D'après (3), les longueurs des côtés de chaque nouveau triangle sont à chaque fois divisée par 2. Appliquons (5) : il existe un entier  n tel que la longueur tn du plus grand côté de Tn soit inférieure à t. Il résulte de (1) et de (2) que les sommets de Q sont intérieurs à chacun des triangles T1, T2, T3, ... donc intérieurs à Tn. On a donc t¾ tn, d'après (4). Contradiction. L'hypothèse (H) ayant conduit à une contradiction, elle est fausse. CQFD.

Théorème 2. La somme de deux entiers naturels pairs est paire.

Preuve 1

Problème 3 Les étiquettes des 10 clefs des 10 chambres de l'hôtel ont été mélangées. On suppose que chaque clef n'ouvre qu'une porte. Combien d'essais au minimum vous permettront de remettre les étiquettes à la bonne place ?

Réponse : 45

Preuve : Deux stratégies simples peuvent être envisagées : on se place du point de vue d'une clef donnée ou du point de vue d'une porte donnée. Dans le premier cas, on fait des essais successifs avec la même clef jusqu'à trouver la porte qu'elle ouvre. Dans le second, on reste devant la même porte et on essaye successivement les clefs jusqu'à trouver la bonne.

Examinons la première manière : 10 essais semblent nécessaires. Mais 9 essais suffisent : en effet, l'énoncé garantissant que toute porte s'ouvre avec l'une des clefs, chaque clef ouvre l'une des portes; ainsi, après 9 essais infructueux d'une clef donnée, on est sûr qu'elle ouvre la porte restante.

Une fois qu'un bon appariement est établi, il suffit de résoudre le même problème avec une clef de moins et une porte de moins. En fin de compte, 9+8+7+...+1 = 45 essais suffisent.

L'autre stratégie conduit à un raisonnement analogue et au même résultat.

Peut-on faire mieux ? Non ! En effet, il n'y a que deux façons d'être certain qu'une clef C ouvre une porte P sans en faire l'essai direct : soit on le déduit du fait que C n'ouvre aucune des 9 autres portes. Soit on le déduit du fait que P n'est ouverte par aucune des autres clefs. Ainsi, dans le pire des cas, 9 essais infructueux sont nécessaires. De même 8 essais infructueux seront nécessaires pour identifier un second appariement, 7 pour un troisième, etc., soit 45 essais au total. CQFD.

Théorème 4 (les 3 maisons et les 3 usines). Dans un plan, il est impossible de relier par des lignes continues 3 points distincts à 3 autres points distincts sans qu'au moins deux des lignes se croisent.

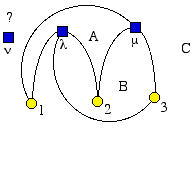Preuve On dessine une solution partielle avec 2 maisons et 3 usines ; cela détermine 3 régions A,B,C Quelle que soit la position que l'on choisisse pour la troisième maison, cette maison sera séparée d'une usine (car chaque usine se trouve à l'extérieur d'une des trois régions).

Problème 5. La situation (1) présente 5 chaînes de 3 maillons enlacés. Ouvrir puis refermer un maillon coûte 100 drachmes. Quel est le prix minimum à payer pour obtenir une chaîne unique de 15 maillons (situation (2)) ?

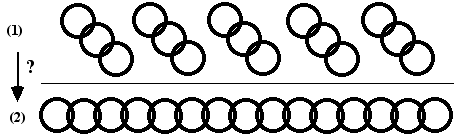
Réponse : 400 drachmes.

Preuve L'ouverture des maillons 4, 7, 10 et 13 et leur accrochage aux maillons 3, 4, 5 et 6, respectivement , fournit une solution avec 4 opérations. Pour voir qu'on ne peut faire mieux, il suffit de considérer l'évolution du nombre total n de morceaux de chaîne : lors d'un accrochage quelconque d'un morceau avec un autre morceau, n diminue de 1. Pour passer de la situation (1) (où n=5) à la situation (2) (où n=1) il faut donc au moins 5-1=4 opérations. CQFD.

Problème 6 Dans un jeu télévisé, le candidat gagnera le contenu d'un coffre qu'il va choisir au hasard parmi trois possibles. Le présentateur précise que deux coffres sont vides et que le troisième contient 1 million de drachmes. Après le choix du candidat, mais avant qu'il ait ouvert le coffre, le présentateur augmente le suspense en montrant au public(candidat compris) que l'un des coffres non choisi est vide. Il offre alors au candidat l'ultime possibilité de modifier, s'il le désire, son choix initial. Que doit faire le candidat pour avoir le plus de chances de gagner ?

Réponse : Il doit changer d'avis.

Preuve. Si vous gardez votre choix initial, vous avez 1 chance sur 3 de gagner. Que se passe-t-il si vous modifiez votre choix ? Imaginez qu'un compère fictif participe simultanément au jeu en gardant son choix initial alors que vous, vous changez. Il est certain que l'un (et un seul ) des deux va gagner. La probabilité de votre compère étant de 1/3, la votre est de 2/3.

Problème 7 (classe de 3ème) Résoudre dans R l'équation (E) x²+x+1=0

Solution 0 n'est pas solution. On peut donc diviser par x les deux membres de (E). On obtient x+1+1/x = 0 ou 1/x= -1-x, d'où, en utilisant l'équation (E), 1/x=x², soit x³=1. La solution est donc x=1. Donc 3= 1²+1+1=0.

Critique de la solution : Il faut raisonner par analyse et synthèse en distinguant bien entre équation et égalité et en utilisant le plus possible des équations équivalentes. Cela donne :

1) Analyse. Si a est solution, alors a=1. ; 2) Synthèse. Donc (E) n'a aucune solution.

Théorème 8. On ne peut mettre plus de 4 rois dans un échiquier 4¥4 sans que deux rois soient en prise mutuelle .

Preuve. On divise l'échiquier en 4 morceaux, chacun étant un échiquier 2¥2. Si on met 5 rois dans un 4¥4, au moins 2 d'entre eux seront dans le même morceau. C'est absurde car, dans un 2¥2, on ne peut mettre qu'un roi.

Critique de la preuve. " Je ne suis pas convaincu(e), car il faut tenir compte des frontières : lorsqu'on réassemble les morceaux, les rois des différents morceaux peuvent interférer. "

Théorème 9. Si les sommets d'un polygone régulier P sont sur un quadrillage, P est un carré.

Preuve. Nous montrons le théorème pour les polygônes convexes (cela suffit). Nous pouvons ainsi parler sans ambiguité d'intérieur et d'extérieur. Pour tout polygone P du plan (à n„3 cotés) , on notera q(P) le nombre de points du quadrillage situés à l'intérieur de P. On appelle nombre n-régulier tout nombre de la forme q(P) où P est un polygone régulier à n cotés (polygone conservé par rotation d'angle 2/n autour d'un point appelé son centre) dont les n sommets sont sur un quadrillage.

On rappelle tout d'abord un axiome fondamental (axiome de récurrence) gouvernant les nombres entiers naturels:

(1) Toute succession strictement décroissante de nombres entiers naturels est finie.

On établit ensuite sans difficulté le lemme suivant :

(2) Si deux sommets consécutifs d'un carré sont sur le quadrillage, les deux autres sommets aussi.

Faisons l'hypothèse (H) : il existe un nombre n-régulier. Soit alors q(P1) un nombre n-régulier quelconque, correspondant à un polygone régulier à n côtés P1 dont les sommets sont sur un quadrillage. Si A et B sont deux sommets consécutifs de ce polygone P1 (orienté dans le sens positif), soit B2 le point obtenu à partir de B par une rotation de/2 autour de A ( voir figure 1).

Figure 1

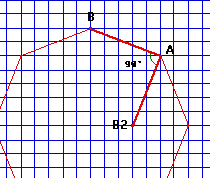En répétant cette construction pour chaque coté de P1, on obtient les n sommets d'un polygone P2. On fait alors les observations suivantes : - Il résulte de (2) que les sommets de P2 sont encore sur le quadrillage. - Toute transformation qui conserve les sommets du polygone P1 conserve aussi ceux du polygone transformé P2. Ainsi, P1 étant régulier (c'est-à-dire conservé par rotation), P2 l'est aussi. - Si n>4, le point B2, et donc le polygone P2 est à l'intérieur de P1. On a donc q(P2)<q(P1). Nous avons donc établi le lemme suivant : (3) Pour tout nombre n-régulier, il existe un nombre n-régulier plus petit. Cette propriété contredit (1). L'hypothèse (H) est donc absurde pour n>4.

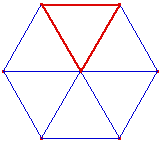
Que se passe-t-il pour n=3. ? Si un triangle équilatéral avait ses sommets sur un quadrillage, on pourrait former un hexagone régulier ayant ses sommets sur le quadrillage (voir figure 2 : dès que trois sommets d'un parallélogramme sont sur un quadrillage, le quatrième sommet aussi), ce qui est impossible, comme nous venons de le voir. Cela complète la preuve du théorème.

Figure 2

Théorème 10 (des "calissons"). Le calisson est une friandise à base de pâte d'amande, une spécialité d'Aix en Provence dans le midi de la France. Sa forme est celle d'un losange obtenu en accolant deux triangles équilatéraux égaux. Avec des calissons identiques de côté 1 on peut remplir une boite régulière hexagonale dont le côté est un nombre entier n quelconque. Les calissons utilisés se répartissent alors en trois groupes, suivant leur orientation. Quelque soit le rangement proposé, les trois groupes comportent le même nombre de calissons.

Preuve Une magnifique preuve virtuelle de ce théorème est fournie par la figure ci-contre : en colorant les calissons suivant leur orientation, on met en évidence un empilement de cubes !

Théorème 11 On désire parcourir une fois et une seule les 100 cases d'un damier 10x10 en démarrant sur une case de coin et en terminant sur le coin opposé. Les seuls déplacement autorisés consistent à passer d'une case à l'une de ses cases voisines. Un tel parcours est impossible.

Preuve : Par l'absurde: supposons qu'un tel parcours existe. Considérons la coloration usuelle des cases du damier en noir et blanc. A chaque mouvement élémentaire, la case occupée change de couleur. Le parcours cherché comporte un nombre pair de cases: case d'arrivée et case de départ ont donc des couleurs différentes. Deux coins opposés étant de même couleur, on a une contradiction. CQFD. Critique de preuve (1) Ce raisonnement n'est pas probant : et si on colorait autrement ? Critique de preuve (2). Gardons la même coloration en damier mais déformons le damier de manière à former un morceau de cylindre : on juxtapose le bord gauche des cases 11,21,...,91 avec le bord droit des cases 10, 20,..., 90 (voir la figure ) . En appliquant la preuve précédente on conclut à l'impossibilité d'un parcours complet commençant en 1 et finissant en 100. C'est faux ! Un tel parcours existe 1,2,...,10,11,...,20,21,...,etc. jusqu'à 100.

Théorème 12 (Pythagore) (classe de 4ème). Un carré construit sur l'hypoténuse a une aire égale à la somme des aires des carrés construits sur les deux autres cotés.

Preuve

Problème 13. (classe de 1ère). La variable x désignant la mesure d'un angle exprimée en degrés, quelle est la limite de sinx/x lorsque x tend vers 0 ?

Réponse D'après le cours, la limite de sinx/x vaut 1 lorsque x est exprimé en radians. La mesure en radians d'un angle de x° est X= x x180/.
En convertissant en radians l'expression sinx/x on obtient  (180/) sinX/X. Comme X tend vers 0 avec x, la limite cherchée est (180/).

Critique de la réponse. " La limite d'une fonction ne peut dépendre des unités choisies ! (Par contre, le graphe de la fonction, lui, en dépend) ".

Problème 14. Prouver que la somme des angles d'un polygone plan non croisé ne dépend que de son nombre de côtés et ne dépend pas de sa forme (les angles sont mesurés à un tour complet près).

Preuve. Découpons le polygone en triangles. Si n désigne le nombre de sommets, le nombre de triangles utilisés est n-2. Un angle en un sommet A du polygone se décompose en la somme des angles de même sommet dans les triangles qui contiennent A. La somme des angles du polygone est donc égale à la somme des angles de tous les triangles, soit (n-2).

Problème 15 (Site "Mathématiques amusantes" , http://carredas.free.fr)

Trois mathématiciens A B C jouent à un jeu. Un arbitre dispose de huit timbres : 4 rouges et 4 verts. Il colle 2 timbres au hasard sur le front de chacun des mathématiciens et garde les deux timbres restants dans sa poche. La situation est telle que chaque mathématicien est incapable de voir les timbres qu'il a sur le front, pas plus qu'il ne connaît les timbres gardés par l'arbitre. En revanche chacun voit les timbres collés sur le front de ses comparses.

L'arbitre demande tour à tour à chacun s'il est capable de deviner les timbres qu'il a sur le front. Voici leur réponse dans l'ordre:

A : Non, B : Non, C : Non, A : Non

Que vont répondre B puis C maintenant ?

Réponse (Site "Mathématiques amusantes" , http://carredas.free.fr)

Yeah! Voila un problème interessant! Il est proche mais différent du problème des timbres de la page du Croco (chez mygale). En fait il est beaucoup plus intéressant car on a encore moins d'informations au départ.

1°) Commencons par montrer, grâce a un raisonnement par l'absurde, que B ne peut pas avoir deux timbres identiques.

Supposons donc que B a deux timbres de la même couleur, par exemple deux timbres rouges: RR. Si C avait aussi RR, alors A en déduirait immédiatement qu'il a VV. Inversement si A avait aussi RR, c'est C qui déduirait immédiatement qu'il a VV.

Donc A et C ont au moins un timbre V chacun. Mais ils ne peuvent pas avoir tous les deux VV, car sinon B saurait tout de suite qu'il a RR.

Il reste 3 cas à considérer:

A=VV, B=RR, C=RV

A=RV, B=RR, C=VV

A=RV, B=RR, C=RV

Le premier cas est impossible car alors C, ayant entendu A et B dire non, saurait qu'il n'a ni RR (A aurait dit Oui), ni VV (B aurait dit Oui), et C doit donc dire Oui.

De la même maniere, les deux autres cas sont impossibles car c'est A qui, ayant entendu B et C répondre Non, devrait répondre Oui.

2°) Bien évidemment, si B avait VV le raisonnement serait le même pour expliquer que l'on arrive dans tous les cas à une contradiction.

3°) Tous les cas ont été éliminés, par conséquent B a forcement deux timbres differents, RV. Puisque nous, qui ne voyons pas les timbres, avons su le prouver, à plus forte raison B qui les voit ne peut que le constater. La deuxième réponse de B est donc: OUI !

4°) Sachant que B=RV, il y a 7 cas possibles:

1. A=RR, B=RV, C=VV

2. A=RR, B=RV, C=RV

3. A=VV, B=RV, C=RR

4. A=VV, B=RV, C=RV

5. A=RV, B=RV, C=RR

6. A=RV, B=RV, C=VV

7. A=RV, B=RV, C=RV

Or C ne peut pas distinguer les cas 1 et 2, ni les cas 3 et 4, ni les cas 5, 6 et 7. Il ne peut donc répondre que NON a la dernière question. Par ailleurs, si on continuait à interroger les trois personnes, chacun resterait sur sa position: A et C ne peuvent ni l'un ni l'autre savoir ce qu'il a sur le front, alors que B le sait.

En résumé, B répondra "OUI j'ai un timbre rouge et un timbre vert", et C répondra "NON je n'en sais toujours rien".

Théorème, démonstration, preuve : trois avatars autour d'un même concept

Un théorème est un texte mathématique M qui

- se présente sous la forme suivante :

« D'après L(règles logiques) , dans T (théorie mathématique), si H (ensemble des hypothèses du théorème), Alors C (conclusion du théorème). »

- et pour lequel il existe une démonstration mathématique.

Une démonstration mathématique du théorème M est une succession d'énoncés dont le dernier est la conclusion C de M et tels que chacun d'eux est :

- soit un axiome ou un théorème de T,

- soit une hypothèse de H,

- soit une conséquence logique (au sens de L) d'autres énoncés, apparus plus tôt dans la démonstration.

Dans une démonstration, chaque énoncé particulier apparaît donc comme lié à un ou plusieurs énoncés antérieurs à lui, dont il est une conséquence, et lié à un ou plusieurs énoncés postérieurs à lui, dont il constitue un argument.

Une démonstration est donc, au delà de son apparence linéaire bien ordonnée, un réseau complexe de liens déductifs et argumentatifs entre des énoncés.

Une preuve mathématique est un discours qui, à propos d'un énoncé précis, convainc une communauté mathématique de l'existence d'une démonstration complète de cet énoncé. (On donne aussi le nom de preuve à l'activité de production d'une telle preuve mathématique.)

Nous élargissons ici deux conceptions courantes de la preuve qui voudraient qu'une preuve convainque de la vérité d'un énoncé (moyennant certaines hypothèses) ou qu'une preuve soit une démonstration en elle-même.

- Une preuve a effectivement pour effet de convaincre d'une "vérité", de la validité d'un théorème, mais la connaissance apportée par une preuve, son contenu, est autrement plus riche que le théorème qu'elle établit : l'objet véritable, l'objet essentiel et significatif d'une preuve est la structure du réseau déductif sous-jacent, de la démonstration qu'elle fournit.

- La démonstration d'un théorème n'est jamais complètement donnée par sa preuve : la plupart des éléments sont implicites (volontairement ou non), par souci d'efficacité, de concision et de clarté. Les étapes marquantes qui indiquent l'ossature générale sont explicitées et justifiées, de nombreux autres points étant simplement admis, ou omis. Chez les professionnels, seuls sont présentés les ingédrients qui permettent aux destinataires de la preuve de reconstituer (en pratique ou en théorie) l'ordonnancement démonstratif complet. (On remarquera, dans les textes de professionnels, mais aussi pour les preuves scolaires courantes, que l'ossature générale d'une démonstration apparaît plus souvent à la faveur des sauts, des discontinuités qui émaillent le discours que par l'enchaînement linéaire des explications : ces ruptures, souvent liées à une idée importante, sont d'autant plus significatives et convainquantes qu'elles forcent le lecteur à reconstruire les maillons manquants.)

Preuve, apprentissage et recherche

L'activité de preuve structure l'activité de recherche du mathématicien. Elle consiste essentiellement à concevoir puis à bâtir des architectures déductives qui expliquent à quelles conditions un énoncé conjectural sera valide. Dans son travail, le mathématicien procède le plus souvent "à reculons", de l'énoncé vers la preuve et non des hypothèses vers la conclusion.

De même dans des ateliers de recherches pour "amateurs", comme ceux de MATh.en.JEANS, les étudiants travaillent à justifier peu à peu leurs résultats. Au fur et à mesure des discussions critiques et des reformulations, ils réunissent (en questionnant, en se documentant ou en imaginant...) les ingrédients et outils nécessaires aux démonstrations mathématiques : principes logiques, définitions et connaissances utilisées, hypothèses faites, rédaction d'énoncés intermédiaires (arguments et conséquences), ordonnancement des étapes.

La "théorie" ("le cours") au lieu d'être donnée a priori et avant des "exercices d'applications", apparaît alors comme un aboutissement de l'activité de recherche et, a posteriori, comme un cadre constructif auquel le résultat donne sens et pertinence.

Nul doute que les 15 situations présentées ci-dessus s'éclaireront elles-aussi peu à peu, pour peu que vous les abordiez comme des situations-recherche, et en discutiez. Auquel cas vous pourrez tester vos nouvelles connaissances avec les "exercices" suivants.

Exercice. Discutez la phrase, souvent entendue chez les élèves (au moins en France) : "il n'y a pas de démonstration en Algèbre".

Exercice. Démontrer l'existence d'un triangle équilatéral, d'un carré, d'un polygone régulier à 5 cotés, à 7 cotés, à  n cotés.

ALIBERT D., GRENIER D., LEGRAND M., RICHARD F., L'introduction du débat scientifique à l'intérieur du cours pour provoquer chez les étudiants un processus de découverte et de preuve. Actes de la IVe École d'été de Didactique des Mathématiques et de l'Informatique. Orléans, 30 Juin-5 Juillet. (1986)

LEGRAND M. (1989) Rationalité et démonstration mathématiques, le rapport de la classe à une communauté scientifique. Recherches en Didactique des Mathématiques vol. 9 n°3, 1989, 365-406.

LAKATOS I.- Preuves et Réfutations, édition française (en collaboration avec N. Balacheff) de l'ouvrage de I. Lakatos (Proofs and Refutations, Cambridge University Press), Hermann, Paris 1984.

PAYAN Charles, Une belle histoire de polygones et de pixels, Actes Math.en.Jeans, 1992, 99-105.

Pour une intrusion plus spécialisée dans l'immense littérature actuelle sur la preuve mathématique, on peut consulter avec profit La lettre de la preuve, site WeB édité par Nicolas Balacheff : http://www-didactique.imag.fr/preuve .

Comptes Rendus MATh.en.JEANS 98-06

© MATh.en.JEANS 1998,2001. Tous droits réservés.