Comptes Rendus MATh.en.JEANS 91-02

Enseignante : Elisabeth BUSSER (lycée Bartholdi).

Chercheur (correspondant) : Charles PAYAN (LSD2, CNRS, Grenoble).

Atelier MATh.en.JEANS du lycée Bartholdi à Colmar (68) en 1990-91.

---

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]

[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

---

[Le sujet initial. L'algorithme de Kaprekar]

On part d'un nombre 4 chiffres N. En rangeant les chiffres par ordre décroissant on obtient un nombre A. En les rangeant par ordre croissant on obtient un nombre B. En complétant éventuellement la différence A-B par des 0 à gauche, on obtient un nouveau nombre de quatre chiffres f(N).

• Étudier le comportement de la suite N, f(N), f(f(N)), f(f(f(N))),...

KAPREKAR

KAPREKAR, vous avez dit KAPREKAR ? Mais qui est-ce donc, KAPREKAR ??... mystère !!!

Mathématicien hongrois selon certains, indien selon d'autres, Kaprekar a pourtant laissé son nom à un des plus célèbres et stupéfiants algorithmes. Se composant en tout et pour tout d'une opération de soustraction, cet algorithme a longtemps intrigué et intrigue toujours encore nombre de mathématiciens et informaticiens. Jugez-en vous-même.

1. Prendre un nombre X de 4 chiffres, c'est-à-dire compris entre 0 et 9999 (NB : 74 peut s'écrire 0074).
2. Arranger par ordre décroissant les chiffres de X et le coder sous la forme abcd tel que a b c d.
3. Arranger maintenant les chiffres de X par ordre croissant. On obtient dcba tel que d c b a.
4. Calculer la différence Y de abcd - dcba (Y est un nombre de quatre chiffres).
5. Refaire toutes les opérations à partir de 2. en remplaçant X par Y.

Tel est, en quelques mots, le principe on ne peut plus simple de l'algorithme de Kaprekar. Mais qu'y a-t-il donc de si surprenant dans tout cela, nous direz-vous ? Eh bien,

[Théorème]

Quel que soit le nombre X choisi [sauf ceux de la forme aaaa, voir la remarque ci-dessous], Y finit toujours par tomber sur le nombre 6 174, et y rester (en effet, si l'on applique l'algorithme ci-dessus :

    7 6 4 1
-   1 4 6 7
=   6 1 7 4 )

De plus, ce résultat apparait au bout de 8 tours maximum.

Remarque. Tous les nombres de quatre chiffres ne donnent pas 6 174 par l'algorithme de KAPREKAR. Ce sont tous les nombres de la forme aaaa ([0000], 1111, 2222, Š) et qui donnent un résultat nul. Notre étude se limite donc à 9990 nombres.

Quelques programmes

Malgré sa simplicité d'exécution, l'algorithme de Kaprekar devient vite lassant. Nous avons donc mis au point quelques programmes qui, décomposant, ordonnant puis soustrayant les nombres à notre place, nous rendaient le travail plus facile !

Au bout d'un moment, nous avons remarqué que durant le déroulement des programmes, certains nombres apparaissaient plus souvent que d'autres. C'est le cas par exemple de 8532, 7641 ou encore 6642.

Nous nous sommes alors intéressés aux propriétés du nombre Y en général, c'est-à-dire à la différence abcd - dcba.

Propriétés du nombre Y

Soit X un nombre à quatre chiffres abcd et Y la différence abcd - dcba, avec les conditions décrites plus haut. Effectuons alors :

    a b c d
-   d c b a
=  A B C D

- « d moins a » : ça ne va pas car a > d [sinon les 4 chiffres seraient égaux]. Calculons donc (d + 10) - a = D et retenons 1.

- « c moins (b + 1) » : b c ainsi b + 1 > c. Calculons alors (c + 10) - (b + 1) = C, c'est-à-dire c - b + 9 = C et retenons 1.

- « b moins (c + 1) » : deux cas se présentent :

1°) b < (c + 1). Cela signifie queb = c car bc. [On a alors] (b + 10)-(c + 1)=B.
2°) b(c + 1). On a   b - (c + 1) = B.

* « a moins d » : deux cas à nouveau [les mêmes].

1°) b < (c + 1). [On a] (b + 10) - (c + 1) = B, donc a - (d + 1) = A à cause de la retenue.
2°) b(c + 1). Donc a - d = A, tout simplement.

Etudions maintenant les systèmes obtenus :

Si bc+1

d + 10 - a = D a - d = A c - b + 9 = C b - c - 1 = B

A + D = 10 B + C = 8

Si b < c+1

d + 10 - a = D a - (d + 1) = A b +10 - (c + 1) = B c - b + 9 = C

A + D = 9 B + C = 18

Conclusion

• Pour b > c, [ on a] A + D = 10 et B + C = 8 .
• Pour b c, A + D = 9 et B = C = 9.
  

Un programme

Nous venons donc de prouver qu'au bout d'un tour d'algorithme, le nombre choisi prend une forme ABCD telle que

A + D = 10 et B + C = 8,    ou
A + D = 9  et B = C = 9.

Grace à cette information, nous allons pouvoir prouver que tous les nombres retombent à la fin sur 6 174.

Mais avant tout, nous faisons un programme nous permettant de retrouver les nombres répondant aux propriétés de Y obtenues. Nous obtenons une série de 90 nombres.

Cependant, il n'est pas nécessaire d'étudier tous les nombres, car deux ou trois nombres comportant les mêmes chiffres donnent le même résultat par l'algorithme (ex : 1 359 et 9 531).

Ainsi, après élimination, il ne subsiste que 30 nombres [les "nombres-tests", dont les chiffres sont en ordre décroissant].

L'arbre de Kaprekar

Il ne nous reste maintenant plus qu'à effectuer l'algorithme pour chacun de ces nombres [nombres-tests]. On obtient alors un arbre où l'on remarque que chaque nombre vient "s'emboîter" dans un autre, pour donner à la fin, bien entendu, 6 174.

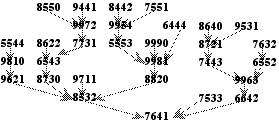
Conclusion

Grace à l'arbre ci-dessus, nous avons la preuve que tous les nombres convergent vers 6 174, et en huit tours au maximum &emdash; car les 30 nombres trouvés, d'après la propriété de Y, apparaissent dès le premier tour de l'algorithme.

Application pratique ? Cette propriété de "convergence", d'après les spécialistes de la numération (informaticiens et mathématiciens) pourrait permettre l'élaboration de nouveaux langages informatiques, ainsi que de nouvelles méthodes de calcul, basées sur la proportionalité de nombres passant par les différentes branches de l'arbre, mais ça Š c'est une autre histoire ! [note 1]

1. Il est facile d'appliquer l'algorithme de Kaprekar avec desnombres de plus de 4 chiffres. Y a-t-il toujours une propriété de "convergence" ?

retour à l'appel de cette note

NOMBRE ENTIER / CHIFFRES / ALGORITHME DE KAPREKAR / SOUSTRACTION / CONVERGENCE / ITÉRATION