
sujet 1 : Le problème des pavages par losanges
On cherche à savoir si une figure
formée de triangles équilatéraux est "pavable" au
moyen de losanges.
C'est à dire, étant donné
un ensemble de triangle équilatéraux positionnés régulièrement,
est-il possible de les recouvrir entièrement et sans chevauchement
au moyen de losanges formés de deux triangles accolés réunis
:

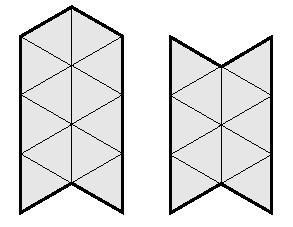
Voici une figure pour tester le critère :
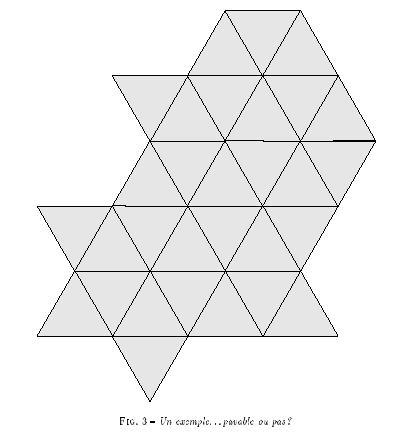
sujet 2 : Les diamands azteques
La figure suivante est un diamand azteque :
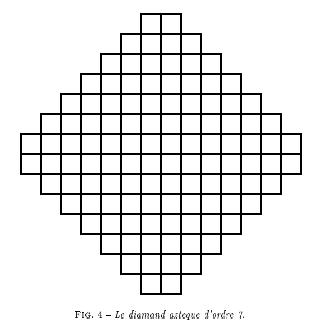
Première étape : montrer qu'un diamand azteque est pavable par des dominos verticaux et horizontaux
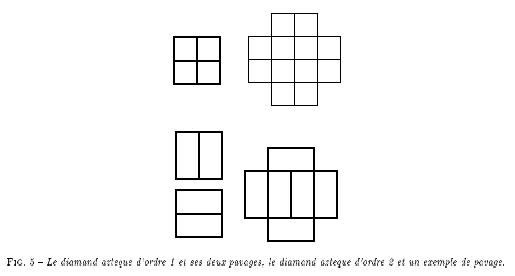
Deuxième étape : Pour un ordre
donné, calculer le nombre de pavages possibles (par exemple, pour
l'ordre 1, il existe 2 pavages possibles, indiqués dans la figure
précédente).