Lycée Paul Éluard (93 - St Denis)
Lycée Étienne Bézout [77 - Nemours]
 

Sujet 1 : Le problème des gardiens de musée.(the art-gallery problem)

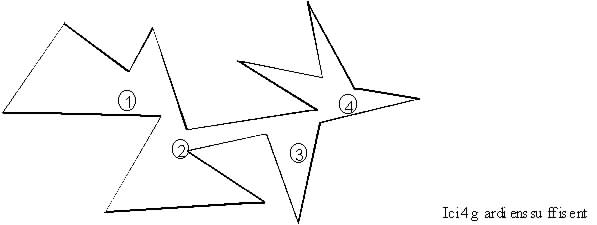
Le problème est de minimiser le nombre de gardiens nécessaires à la surveillance d'un musée modélisé par une forme polygonale plane.

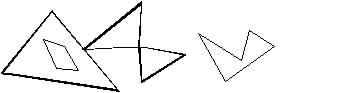
On peut définir une forme polygonale comme une surface formée par la réunion de surfaces triangulaires. On notera que cette définition est formellement plus simple que la définition usuelle mais qu'elle permet des trous et des formes un peu originales :

+ Peut-on trouver une méthode systématique (par exemple un algorithme) qui donne une solution satisfaisante ?

+ Comment être sûr qu'une solution est la meilleure possible ?

+ Combien de gardiens suffisent en général pour un musée qui a n murs ?

+ Pour un musée de l'espace, tridimensionnel, que peut-on proposer ?
 

Sujet 2 :  Le flocon de Von Koch

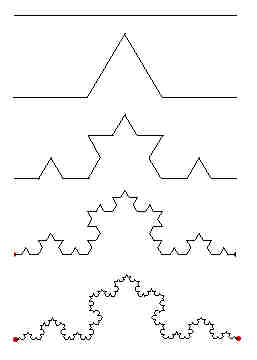La fabrication du flocon de Von Koch est simple à comprendre. Le tiers médian d'un segment est remplacé par les deux autres cotés du triangle équilatéral qui s'appuie sur lui (vers l e haut). On recommence la même opération avec chaque segment de la nouvelle figure . Et on recommence, …, ainsi de suite indéfiniment. La ligne brisée se brise un peu plus à chaque étape. En poursuivant indéfiniment la construction, on observe qu'un contour se précise de plus en plus:  le flocon de Von Koch. Quel est cet objet étrange ? (On parle de "fractale")

+ Le flocon de Von Koch est-il vraiment une "courbe" : peut-on le parcourir d'une extrémité à l'autre ?
Pour cela, on voudrait à chaque instant (mesuré par un nombre réel compris entre 0 et 1) définir une position (un point précis du flocon) de manière à avoir un déplacement continu [c' est dire que pour connaître la position à un instant t avec une précision donnée, il suffit de disposer de suffisamment de décimales pour t].
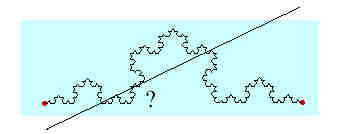
+ Qu'obtient-on si on coupe le flocon par une droite : un point, plusieurs points, une infinité de points ?
+ Inventez vos propres fractales … Imitez la nature ou créez…

Le flocon de Von Koch est-il une courbe ?
Comment une droite le coupe-t-elle ?

Les fractales sont des objet géométriques dont les formes sont similaires quelque soit le grossissement avec lequel on les regarde. Ils permettre d'expliquer modéliser beaucoup de formes observées dans la nature : les nuages, les côtes de Bretagne, les arbres, les alvéoles pulmonaires, les montagnes, les cristaux de neige… Bien d'autres phénomène naturel, moins visibles, obéissent à des lois fractales : par exemple l'atmosphère terrestre ou plus généralement, le mouvement des molécules dans un fluide turbulent.
On peut voir certaines fractales comme des objets intermédiaires entre les objets linéaires "unidimensionnels" et des objets plans, bidimensionnels. Pour mesurer ces fractales, on fait intervenir un nombre qui généralise les propriétés usuelles de la dimension (quant on grossit 3 fois une ligne unidimensionnelle, sa longueur est multiplié par 3, quand il s'agit d'une surface, son aire est multipliée par 9 = 3² , les volumes sont multipliés par 27 = 3³ ) . Ce nombre, baptisé "dimension fractale", est compris entre 1 et 2.
 
 

retour à la liste