Bébé ver de terre dort dans
n'importe quelle position. Sa mère voudrait tricoter une couverture
qui permette de le couvrir entièrement, quelle que soit la position
du petit. Par souci d'économie, elle voudrait que cette couverture
soit de surface aussi petite que possible.
Question : Y-a-t-il une couverture idéale,
et quelle est elle ? (ou quelles sont-elles ?)
Palindrome : mot qui reste inchangé
quand on le lit de droite à gauche : KAYAK est un palindrome, CANOE
n'en est pas un (image miroir : EONAC).
Pour les nombres c'est de même par
exemple 424 est un palindrome 4241 n'en n'est pas un.
Partons d'un nombre, et additionnons-lui
son image miroir :
421 + 124 = 545 est un palindrome
678 + 876 = 1554
1554 + 4551 = 6105
6105 + 5016 = 11121
11121 + 12111 = 23232 est un palindrome
Question : est-il vrai que, quel que soit
le nombre de départ choisi, on aboutit toujours, en répétant
suffisamment longtemps l'opération, à un palindrome ?
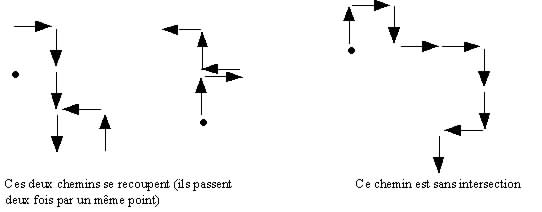
On se place sur une grille carrée, sur laquelle on choisit une origine, un point de départ. Un chemin, formé de pas nord, sud, est et ouest, part de ce point.

Problème : Combien y a-t-il de chemins
de n pas sans intersection ?
| n | 1 | 2 | 3 | 4 |
| Cn | 4 | 4 ×3 = 12 | 12 ×3 = 36 | 36 × 3 - 4 × 2 = 100 |
C'est une question difficile, on ne sait
:
- ni écrire une expression générale
;
- ni écrire une relation de
récurrence satisfaite par les nombres Cn.
Il est également difficile d'écrire
un programme efficace qui calculerait vite C1, C2,
C3, …, C1034, …
(Remarques : A défaut d'attaquer la
question de front, on peut chercher à inventer, à définir,
des familles de chemins plus restreintes et plus faciles à compter.
Par exemple : les chemins qui ne font que des pas Nord et des pas Est)
Sujet 4 : Polyminos
Dominos :![]()
Triminos :![]()
Quadraminos : ![]() etc…
etc…
Question nombre de polyominos à n
plaquettes
| n | 1 | 2 | 3 | 4 |
| Pn | 1 | 2 | 6 | 19 |