|
Pour simplifier nous étudierons les "alphavilles", où les rues forment un quadrillage rectangulaire. Les habitations sont ainsi divisées en "blocs" (à New York, on mesure les distances en blocs). |
|
|
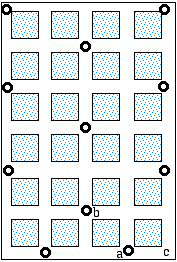
A Alphaville (5 x 7) nous voulons installer des téléphones publics de manière à ce que chaque carrefour soit équipé d'une cabine ou soit voisin d'un carrefour équipé (1 seul bloc de distance). L'ingénieur Godard
propose le plan suivant (figure 1) qui nécessite 11
cabines téléphoniques.
|
 |
|
Nous désirons assurer les secours à Alphaville (6 x 7) en installant le moins posible de casernes à certains carrefours bien choisis. Les pompiers doivent pouvoir intervenir rapidement à n'importe quel carrefour , sans jamais avoir plus de 3 blocs à parcourir. Godard propose le plan suivant (figure ci-contre). - Peut-on obtenir le même résultat avec moins de 4 casernes ?
|

|
Cas général
|
|
Entrées possibles
A quoi cela sert-il ?
Une solution générale de ce problème est toujours cherchée par les mathématiciens. En particulier, le cas des cabines téléphoniques (n= 1) dans alphaville ( p x q) est encore ouvert.
De nombreux problèmes de ce type apparaissent en Recherche Opérationnelle (rationalisation de productions d'ateliers, d'équipements collectifs etc.) et aussi dans les Télécommunications (correction automatique de messages parasités). Leur étude théorique relève de ce qu'on appelle l'Optimisation Combinatoire et de la Théorie des Codes.
|
|
|
|