On peut disposer des graines régulièrement pour dessiner un carré. Avec 9 graines on peut faire 3 rangées de 3., avec 16 graines 4 rangées de 4, avec 25 graines 5 rangées de 5, etc.
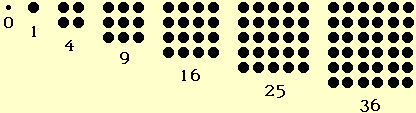
Les nombres 1=1x1, 4=2x2, 9=3x3, 16=4x4, puis 25, 49, 64, 81, 100, etc. sont appelés des nombres carrés (on dit aussi des carrés parfaits ou simplement des carrés : ainsi, 25 est le carré du nombre 5, 64 est le carré du nombre 8 etc. ; on utilise la notation 25= 5^2 = 52, 64 = 8^2 = 82 etc.) .
|
Quelquefois, en ajoutant deux carrés, on obtient un carré plus grand: par exemple (3 fois 3) ajouté à (4 fois 4), donne 9+16=25, c'est à dire 5 fois 5. Lorsque cela arrive, on dit que les trois nombres de base (dans l'exemple ce sont 3, 4 et 5) forment un triplet de Pythagore. Pythagore, mathématicien de la grèce antique, a montré comment fabriquer un angle droit avec un tel triplet : par exemple avec le triplet (3,4,5) on construit un triangle dont les cotés ont pour longueurs 3, 4 et 5 ; l'angle formé par les deux cotés les plus petits est alors droit !
|
|
Les résultats obtenus pourront peut-être aider à résoudre un joli problème de découpage.
|
Les anciens (notamment en Chine antique) connaissaient une autre d'associer des angles droits et des carrés: un carré (géométrique) dont le coté est un nombre entier peut toujours être formé avec des "équerres". Cela illustre une formule simple et jolie : 1 = 1x1 = 1 1+3 = 2x2 1+3+5 = 3x3 1+3+5+7 = 4x4 |
|
etc. De manière générale, on peut écrire : 1+3+5+7+...+(k-ième nombre impair) = kxk.
Cela suggère la question suivante, non résolue à ce jour : lorsque (a,b,c) est un triplet de Pythagore, peut-on toujours réussir à former un carré de coté c en utilisant comme pièces de base les équerres qui forment le carré de coté a et les équerres qui forment le carré de coté b ?
Exemple.
|
Avec deux carrés bien choisis : |
On forme un seul carré : |
  |
 |
Les triplets de Pythagore sont vraiment uniques en leur genre !
Les mathématiciens ont évidemment cherché à généraliser: ils ont cherché des triplets de nombres "cubes" (un nombre cube est de la forme k3= kxkxk), de "puissances quatrièmes" (de la forme k4= kxkxkxk), de "puissances cinquièmes", ... de "puissances n-ièmes" : des cubes qui seraient la somme de deux cubes plus petits, des puissances quatrièmes qui seraient la somme de deux puissances quatrièmes plus petites, etc.
Ils n'en ont pas trouvé. Pierre de Fermat (1601-1665), mathématicien amateur, annonça avoir démontré de manière "vraiment admirable" que de tels triplets n'existent pas. Son raisonnement était-il juste ? Nul ne le sait, car il n'est jamais parvenu jusqu'à nous. C'est seulement en juin 1993 que l'anglais Wiles a pu fournir une telle démonstration d'inexistence, complétée en Octobre 1994 avec l'aide de Taylor. Cette preuve utilise des méthodes très détournées d'inspiration géométrique (cela s'appelle de la Géométrie Algébrique), inventées et mises au point par de nombreux mathématiciens au cours du XXème siècle.
Une question ouverte : les nombres congruents
Il est logique d'appeler triangle pythagoricien un triangle dont les cotés forment un triplet de Pythagore. Un triangle pythagoricien est donc un triangle rectangle dont les cotés sont des nombres entiers.
Plus généralement, on peut s'intéresser aux triangles rectangles rationnels, c'est à dire aux triangles rectangles dont tous les cotés sont des nombres rationnels (des fractions). On peut voir chaque triangle rectangle rationnel comme un modèle réduit d'un triangle pythagoricien, le coefficient de réduction étant un nombre entier.
Exemple : le triangle pythagoricien de cotés 9,40,41 réduit dans un rapport 6 donne le triangle rectangle rationnel de cotés 9/6, 40/6, 41/6, dont l'aire est 5.
Un entier naturel positif est dit congruent s'il mesure l'aire d'un triangle rectangle rationnel. L'exemple précédent montre que 5 est un nombre congruent.
1 est-il un nombre congruent ? Cette question, apparue dans les mathématiques arabes des VIIIe et IXe siècles, ne fut résolue qu'au XVIIIe siècle : Pierre de Ferma