i = rDocument MATh.en.JEANS
Énoncé du principe de Fermat en optique.
O est un point d'observation, S est une source lumineuse, M est un miroir convexe, placé de telle manière que, depuis O, l'on puisse voir l'image de S réfléchie par M.
Alors, le trajet du rayon lumineux qui partant de S arrive en O après réflexion sur M est de longueur minimum, parmi tous les chemins possibles de S à O qui rencontrent M.
Remarque. Pour des raisons géométriques (voir théorème 1 plus bas), un seul rayon lumineux issu de S peut, après réflexion sur M, parvenir à O.
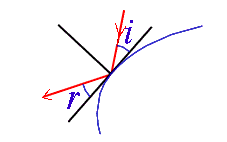
Loi de la réflexion optique.
Lors de la réflexion d'un rayon de lumière sur une surface, il y a égalité entre l'angle d'incidence i et l'angle de réflexion r.
i = rApplication
Un point F tel que la somme FA+FB+FC soit minimum est appelé point de Fermat. Le texte ci-dessous montre comment le principe de Fermat et la loi de réflexion se conjuguent pour donner une propriété caractéristique du "point de Fermat" d'un triangle lorsque ce point est intérieur au triangle : ce point "voit" chaque coté du triangle suivant un angle de 120°.
|
par Jean Lochet, (Université de Bordeaux I), 26 janvier 2002 Supposant qu'il existe, à l'intérieur du
triangle ABC, un point F &endash; dit point de Fermat
&endash; qui minimise la quantité FA + FB + FC, on se
propose d'établir une propriété de ce
point grâce au Principe de Fermat (Optique).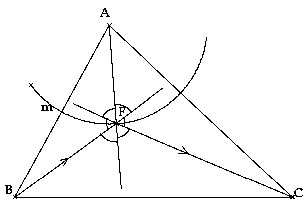 
D'après le Principe de Fermat, le trajet FB + FC, du rayon lumineux issu de B se réfléchissant en F sur m et passant par C, est minimum . Comme AF est la normale en F au miroir m, les lois de la
réflexion impliquent que :
|
Un théorème de géométrie (réciproque du théorème dit de "l'angle capable") dit que l'ensemble des points qui "voient" un segment donné AB sous un angle donné est constitué de deux arcs de cercles d'extrémités A et B, symétriques par rapport au segment [AB].
Il n'est pas difficile d'en déduire que, lorsque les angles du triangle ABC sont tous inférieurs à 120°, il existe un point et un seul qui soit intérieur au triangle et qui "voit" les trois cotés sous le même angle de 120°.
Dans le cas où les angles du triangle sont inférieurs à 120°, le point de Fermat est donc unique, ce qui n'était nullement évident au départ.
Le point de vue Mathématique
Lumière et miroir étant hors du champ mathématique, la traduction mathématique des principes et lois physique souleve plusieurs questions d'inégale importance.
Théorèmes mathématiques sous-jacents
Soit P,Q deux points extérieurs à un domaine convexe D [1] dont le bord B est lisse [2]. Soit M un point du bord (B) de (D) et soit [MN[ la demi-droite normale [2] à (B) en M. Sous ces hypothèses, on a les propriétés suivantes.
PMN et NMQ soient
égaux.
PMN et NMQ sont
égaux, alors la ligne brisée PMQ est un chemin de
longueur minimum parmi les chemins de P à Q qui passent par
un point de D.
PMN et NMQ sont
égaux.
Ce sont l'énoncé n°3 et l'énoncé réciproque n°4 qui traduisent le mieux le principe de Fermat en Optique. C'est l'énoncé n°4 qui servirait à "mathématiser" le texte précédent pour prouver que, si le point de Fermat existe et est intérieur au triangle, alors il voit chaque coté du triangle sous le même angle de 120°.
Notes
1. Un domaine convexe est un ensemble convexe D de points admettant au moins un point intérieur. Dans le plan, il suffit pour cela que D contienne 3 points non alignés. Dans l'espace, il suffit que D contienne 4 points non coplanaires.
retour à l'appel de cette note
2. Dans le plan B est une courbe, dans l'espace B est une surface. Dans chaque cas, on dit que B est lisse si elle admet une tangente (respectivement, un plan tangent). Une courbe lisse (respect. une surface lisse) admet une normale en tout point, qui peut être orientée de manière à "sortir" du domaine D.