Considérons les n premiers entiers non nuls, par exemple 1, 2, 3, 4, 5, 6, 7 pour n = 7. Maintenant, nous allons les mélanger, c’est-à-dire les considérer dans un ordre quelconque, par exemple 2, 3, 6, 1, 5, 7, 4 sur notre exemple.

Nous appelons ce mélange une permutation à 7 éléments : p = 2.3.6.1.5.7.4 (les points seront utiles dès que nous considèrerons des permutations à plus de 9 entiers…).

Nous pouvons représenter notre permutation p graphiquement sous la forme d’un tableau (ci-contre)

Ce tableau est construit de la façon suivante : si le i-ième entier de la permutation p est j, alors nous colorions en gris la case j de la i-ième colonne (par exemple, la case 6 de la 3-ième colonne est ici grise…). Remarquons que chaque ligne et chaque colonne de ce tableau ne contient qu’une seule case grise.

 
• Sauriez-vous dire combien de permutations différentes nous pouvons obtenir avec n entiers ? Sauriez-vous également le prouver ?

Nous appellerons motif, une permutation plus petite, c’est-à-dire une permutation à k éléments avec k < n. Par exemple, la permutation à 3 éléments m = 2.3.1 est un motif (voir ci-contre).

Nous dirons qu’une permutation p contient le motif m, si nous pouvons trouver 3 entiers, pris dans l’ordre de la permutation p, qui " respectent " le motif m. Pour notre motif m = 2.3.1, cela signifie que le premier entier doit être plus petit que le second et plus grand que le troisième.

Exemple. Notre permutation p = 2.3.6.1.5.7.4 contient le motif m = 2.3.1 ; en effet, ce motif se retrouve par exemple avec les entiers 3.6.1, 5.7.4, 6.7.4, et 2.3.1 lui-même ! (En voyez-vous d’autres ?) Elle contient également les motifs 1.2.3 ou 3.2.1 (voyez-vous pourquoi ?).

Finalement, nous dirons qu’une permutation p évite un motif m si elle ne le contient pas ! Par exemple, notre permutation p = 2.3.6.1.5.7.4 évite le motif m’ = 4.3.2.1. Voyez-vous un motif à 3 éléments que notre permutation évite ?

Ce sont ces permutations, qui évitent un certain motif (ou plusieurs), qui vont nous intéresser. Plus précisément, nous aimerions savoir, pour un motif m donné, combien de permutations à n éléments évitent ce motif m…

Sauriez-vous par exemple répondre aux questions suivantes ?

 
• Combien de permutations à n éléments évitent le motif 1.2.3 ? le motif 3.2.1 ?

   

• Combien de permutations à n éléments évitent à la fois le motif 1.2.3 et le motif 3.2.1 ? à la fois le motif 1.2.3 et le motif 1.3.2 ? à la fois le motif 1.3.2 et le motif 2.1.3 ? à la fois le motif 1.2.3 et le motif 2.3.1 ?

   

• Combien de permutations à n éléments évitent à la fois le motif 1.2…k-1.k et le motif k.k-1….2.1 ?

   

• Combien de permutations à n éléments évitent à la fois les motifs 1.2.3, 1.3.2 et 2.1.3 ?

   

• Combien de permutations à n éléments évitent à la fois les motifs 1.2.3, et 1.4.3.2 ?

Pour chacune de ces questions, la technique à utiliser sera la suivante : construire toutes les permutations à n éléments (pour les premières valeurs de n) qui évitent le motif, les compter, essayer de deviner la formule et, si possible, de la prouver !

On peut " inventer " de nombreuses questions dans ce cadre… Par exemple, sauriez-vous construire la plus petite permutation contenant tous les motifs de taille 3 ? de taille 4 ? de taille k ?

1. Que de rectangles !

   Commençons par un petit problème de carrés : nous considérons une grille carrée, de taille nxn, et essayons de compter les carrés " plus petits " que contient cette grille. Par exemple, la grille 3x3 contient 9 carrés de taille 1x1 et 4 carrés de taille 2x2… Ainsi, au total, notre grille 3x3 contient 9+4+1 = 14 carrés. De façon plus générale :

    
   • Combien de carrés de taille kxk contient une grille carrée de taille nxn ?

      

   • Combien de carrés contient au total une grille nxn ?

   Pour chacune de ces questions, la technique à utiliser sera la suivante : compter " à la main " ces carrés pour les premiers cas, essayer de " deviner " une formule et, enfin essayer de la prouver !

   On peut très facilement étendre ce type de questions à d’autres situations, en imaginant de nombreuses variantes. Citons-en quelques-unes :

    
   • Combien de rectangles de taille kxl contient une grille carrée de taille nxn ? combien de rectangles au total ? (n’oublions pas que les carrés sont aussi des rectangles !)

      

   • On peut se poser la même questions pour les grilles rectangulaires de taille nxm…

      

   • On peut rajouter des " trous " dans le rectangle (c’est-à-dire des zones, par exemple rectangulaires, ne contenant pas de case. On pourra dans ce cas commencer par des situations " simples ", par exemple une grille carrée nxn avec un trou central de taille pxp…

   Les seules limites sont alors notre imagination… et notre capacité à obtenir de nouveaux résultats !

   1. La chasse aux cailloux

      Ce jeu se joue sur une grille carrée de taille nxn (décidément !). La case en bas à gauche contient le chasseur (C), et toutes les autres cases contiennent un caillou. Le chasseur doit, en partant de sa case départ, se promener dans la grille, ramasser tous les cailloux, et revenir à son point de départ (il possède un panier pouvant contenir tous les cailloux). Pour se promener, le chasseur peut passer d’une case à l’une des 4 cases (au maximum) voisines : il peut donc faire un pas vers le nord, l’est le sud ou l’ouest.

      ·	·	·	·	·	·
      ·	·	·	·	·	·
      ·	·	·	·	·	·
      ·	·	·	·	·	·
      ·	·	·	·	·	·
      C	·	·	·	·	·

       

      La longueur du chemin parcouru par le chasseur est donnée par le nombre de cases traversées. Une première question, facile, est la suivante :

       
      • En supposant que le chasseur ne doit jamais repasser par une case (sauf la case départ), quelle est la longueur d’un plus court chemin de ramassage ? Sauriez-vous proposer un tel chemin ?

      Il est beaucoup plus intéressant d’autoriser le chasseur à traverser plusieurs fois la même case (il ramasse le caillou lors de son premier passage) et de considérer d’autres types de chemins. Par exemple :

       
      • Sauriez-vous proposer un chemin de ramassage pour lequel le nombre de virages (c’est-à-dire de changements de direction) est minimum ? Quelle est sa longueur ?

         

      • Sauriez-vous résoudre le même problème pour une grille de taille nxn quelconque ?

      Pour chacune de ces questions, la technique à utiliser sera la suivante : construire la " meilleure solution " et essayer de prouver que l’on ne peut effectivement pas faire mieux !

      On peut ensuite considérer de nombreuses variations, par exemple :

       
      • On peut considérer le cas où la case de départ n’est pas nécessairement celle du coin bas-gauche. Dans ce cas, quelle est la case de départ qui donne le meilleur résultat ?

         

      • On peut également considérer le cas où le panier du chasseur ne peut contenir qu’un nombre limité, disons k, de cailloux. Il devra ainsi repasser plusieurs fois par la case départ ! Que peut-on dire alors lorsque k vaut 1, 2 ou un nombre quelconque ?

      On pourra, selon son imagination, proposer d’autres situations : considérer des grilles triangulaires, autoriser des pas diagonaux (lorsque les cases sont voisines par un coin), considérer d’autres types de grilles (par exemples triangulaires, en rajoutant une ou deux diagonales), travailler en dimension 3 ou supérieures, rajouter des " îles " dans la grilles (c’est-à-dire des cases vides que le chasseur n’a pas le droit de traverser), etc.

      1. Nombres géométriques

         On s’intéresse ici à des suites de nombres engendrées par des suites de figures géométriques (d’où la notion de nombres géométriques...).

         Les figures sont obtenues en plaçant des jetons sur des intersections de " réseaux " (ou " quadrillages " particuliers) du plan (infini). Considérons un premier exemple qui va nous aider à mieux comprendre :

         

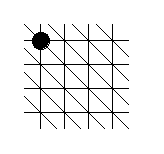
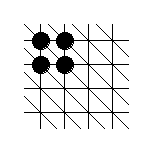
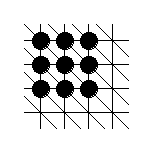
         Chaque intersection de ce réseau possède 6 voisins que l’on peut naturellement qualifier de Nord, Est, Sud-Est, Sud, Ouest et Nord-Ouest (ou, plus simplement, N, E, SE, S, O et NO). Ce réseau est un réseau triangulaire car les cellules de base sont toutes des triangles...

         La règle de construction, dite règle N-O-NO, est la suivante : on démarre avec un seul jeton et, à chaque étape, une intersection ayant une intersection voisine N, O ou NO occupée par un jeton récupère un jeton... La suite de nombres correspondante est obtenue en comptant les jetons : 1, 4, 9, etc. Il est assez facile de se convaincre que le n-ième nombre de cette suite est n² (on comprend pourquoi ces nombres sont appelés des carrés...).

         Au niveau géométrique, une telle suite est caractérisée par trois informations :

          
         • la structure du " réseau " (carrés, triangles, hexagones, ...),

            

         • la figure initiale (un point, un segment, un " L ", un rectangle, ...),

            

         • la règle d’évolution des jetons.

         Pour une telle suite, le problème consiste alors à trouver une formule générale donnant la valeur du n-ième nombre de la suite. Cela peut être simple, comme dans notre exemple, ou plus compliqué...

         Pour commencer, on pourra se limiter à un réseau de type quadrillage (en supprimant les diagonales dans notre exemple), et considérer les questions suivantes :

          
         • en utilisant la règle N-O, qu’obtient-on à partir d’un point ? d’un segment de longueur p ? à partir d’un rectangle p x q ? et ainsi de suite selon votre imagination...

            

         • que se passe-t-il si l’on modifie la règle d’évolution ? Par exemple, avec la règle N-E-S-O ?

         On pourra ensuite considérer le réseau triangulaire vu précédemment (dans notre exemple initial) ou le réseau triangulaire obtenu en rajoutant la deuxième diagonale SO-NE.

         Pour chaque problème, la technique à utiliser est généralement :

          
         • construire graphiquement les premiers nombres,

            

         • essayer de " deviner " la formule,

            

         • démontrer que la formule est correcte !

         Remarquons pur finir que rien ne nous interdit de considérer ensuite des " grilles de dimension 3 ", voire des grilles de dimensions supérieures pour les plus courageux (l’étape qui consiste à " dessiner " les premiers nombres est alors beaucoup plus délicate...).

         1. Le jeu de franc carreau

            Georges Louis Leclerc, comte de Buffon (1707-1788) est essentiellement connu pour son oeuvre de naturaliste, mais il fut aussi philosophe et mathématicien. Il a notamment écrit en 1777 un mémoire sur le " Jeu de franc carreau " qui est à l’origine de ce problème.

            Le jeu de franc carreau se joue sur un sol carrelé de carreaux carrés (sic) de côté C. On jette en l’air une pièce ronde, de diamètre D, qui ne retombe jamais sur la tranche... Le joueur A parie que la pièce retombera à franc carreau (c’est-à-dire qu’elle sera entièrement contenue dans un carreau) et le joueur B parie le contraire (c’est-à-dire qu’elle chevauchera au moins un joint). On suppose pour simplifier que les joints sont " sans épaisseur " et que le sol est " infini "...

            La question est alors :

            Quelle doit être la valeur du côté des carreaux C (en fonction du diamètre de la pièce D) pour que ce jeu soit équitable, c’est-à-dire pour que chaque joueur ait une chance sur deux exactement de l’emporter ?

            Pour résoudre ce problème, il suffit de remarquer que si le centre de la pièce tombe à une distance inférieure ou égale à C-D du centre d’un carreau, elle ne chevauchera aucun joint. Dans le cas contraire, elle chevauchera nécessairement au moins un joint... Ainsi, on peut partager le plan en deux zones : la zone A (qui signifie que le joueur A gagne si le centre de la pièce tombe dans cette zone) et la zone B (qui fait gagner le joueur B). Pour que le jeu soit équitable, il faut donc que ces deux zones aient la même surface...

             
            • Saurez-vous montrer que pour que le jeu soit équitable il faut avoir C =

             ?

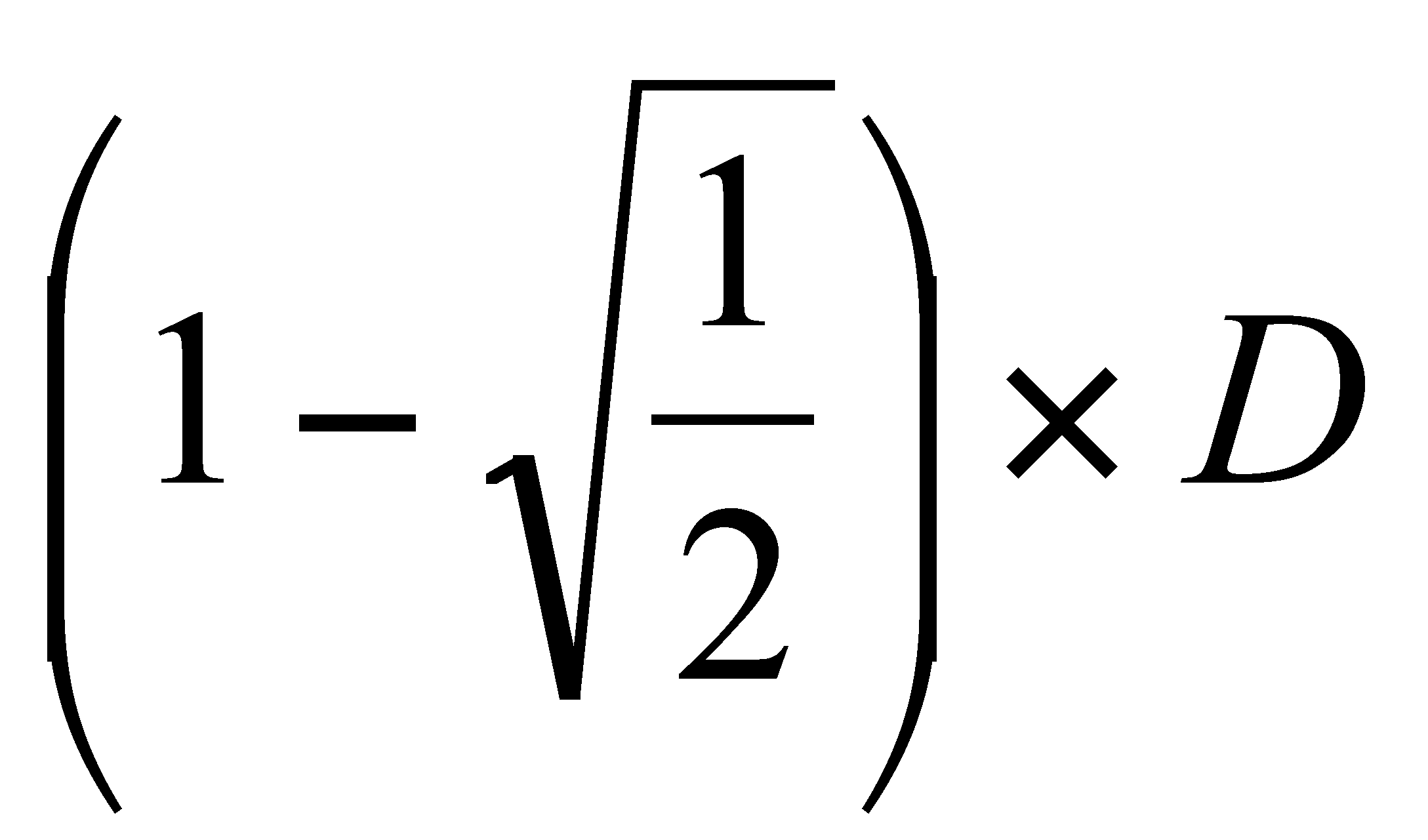
            Plusieurs variantes de ce jeu peuvent être considérées, par exemple :

             
            • Que se passe-t-il si les carreaux sont des triangles équilatéraux ? des hexagones ?

               

            • Que se passe-t-il si la pièce est en forme de carré ? de triangle ? de " L " ?

            Le principe de résolution reste le même, mais les formules obtenues sont naturellement différentes...

            Une autre variante, connue sous le nom de " l’aiguille de Buffon " est la suivante : le jeu se joue sur un parquet cette fois (un ensemble de lignes parallèles espacées d’une distance d) et l’on jette une aiguille de longueur l...

             
            • Saurez-vous trouver la solution de ce problème ? (C’est-à-dire calculer la probabilité de gain de chacun des joueurs en fonction de la distance d et de la longueur l).

            On peut alors considérer, au gré de notre imagination, de nombreuses variantes (par exemple reprendre nos carrelages précédents et y jeter l’aiguille...), chacune donnant lieu à un intéressant problème de géométrie...

             

             

             

            Éric SOPENA

            Chercheur au LaBRI

            sopena@labri.fr