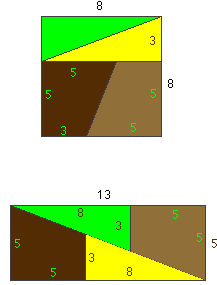
|
Voici un carré de côté 8. |
|
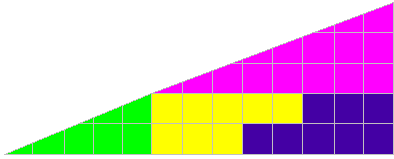
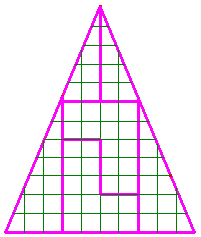
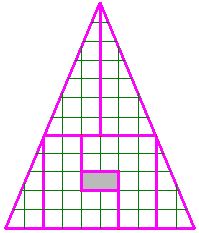
Question 2 : Le triangle de Gardner
|
|
|
Les deux figures ont-elles la même aire ? Pourquoi ?
Question 3 : Autres triangles de Martin Gardner...
Triangles rectangles ou isocèles avec des morceaux réarrangés de manière à former un triangle apparemment identique, mais avec un trou... à vous de jouer !
|
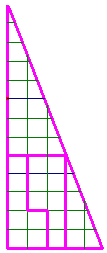
Un triangle rectangle avec un trou de 1 unité. | |
|---|---|
|
|
|
|
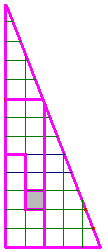
Un triangle isocèle avec un trou de 2 unités. | |
|---|---|
|
|
|
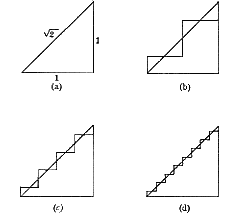
Question 4 : Le paradoxe des gradins
, car le carré de
l'hypoténuse est selon Pythagore :
12 + 12 = 2. La somme des
longueurs des 2 côtés de l'angle droit est 1 +
1 = 2.Si nous construisons une ligne brisée avec des gradins en angle droit comme sur la figure ci-dessous, il est facile de conclure que sa longueur est toujours égale à 2 (les segments verticaux mis bout à bout ont une longueur de 1 et les horizontaux mis bout à bout ont aussi une longueur de 1). En réitérant le procédé, nous avons toujours une ligne brisée de longueur 2. Continuons indéfiniment à augmenter le nombre de gradins, nous obtenons une suite de lignes brisées qui se rapprochent de plus en plus de l'hypoténuse du triangle rectangle. On a bien envie de penser que la ligne brisée se confondra à la fin avec l'hypoténuse et donc que sa longueur sera celle de l'hypoténuse donc !
Nous aurions donc 2 =
?|
On peut tracer la ligne brisée de nombreuses
façons : |
|
Expliquer où est l'erreur de raisonnement.
Question 5 : Le paradoxe de l'euro manquant
|
|
Trois amis vont au restaurant chinois et commande chacun
un plat. Il y en a en tout pour 25 euros. Chacun donne dix
euros et pour faire un compte rond, demande au serveur de
rendre à chacun un euro et de se garder les deux
euros restant comme pourboire. |
Où est passé l'euro manquant ?
Question 6 : Le paradoxe des chameaux
(ou : le bédouin a la bosse des maths).
|
|
|
Par testament, il avait légué :
- la moitié de ses bêtes à l'aîné ;
- le tiers au cadet ;
- le neuvième au benjamin.
Le partage semblant impossible aux héritiers, un vieux sage
bédouin vient à leur secours en leur proposant la
solution suivante :
« Je vous donne mon chameau. Avec 18 animaux, le partage se
fait aisément :
L'aîné aura 18 x 1/2= 9 , le cadet aura 18 x 1/3 = 6 et
le benjamin aura 18 x 1/9 = 2.
Voilà, 9 + 6 + 2 = 17, il reste un chameau, c'est le mien, je
le récupère et vous salue bien » .
Fabriquer toutes les variantes possibles de ce problème, sachant qu'on peut changer le nombre de chameaux, qu'il y a toujours trois fils et que toutes les fractions utilisées sont de type 1/n.
Par exemple, une variante possible est :
11 chameaux : 1/3 pour l'aîné, 1/3 pour le cadet et 1/4 pour le benjamin.
Commentaire de la rédaction :
