Sujet 1. Géométrie non euclidiennes.
[exposé : Géométrie sur des surfaces courbes (constituées de polygones plats) ]
nb d'élèves : 2 (FILZ Emmanuel, REGNIER David)

Dans la nature, les surfaces (par exemple la surface d'un massif de montagnes) sont rarement plates, mais comportent des creux, des bosses, des plis...

On propose d'étudier les propriétés géométriques de surfaces "courbes" particulières, constituées de polygones plats, en premier lieu en s'intéressant à l'exemple de la surface construite de la manière suivante.

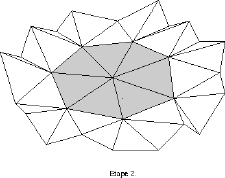
On prend des triangles équilatéraux plats de même taille. On commence par en recoller k=7 autour d'un sommet comme dans le dessin ci-dessous (étape 1).	A l'étape suivante, on recolle des nouveaux triangles autour de chaque sommet de la surface construite de manière à ce qu'il y en ait exactement k autour de chaque sommet (étape 2).
Et ainsi de suite.

• Comment trouver les plus courts chemins entre deux points sur la surface ?
• Sont-il uniques ou peut-il y en avoir plusieurs ?
• Peut-on avoir une idée de la vitesse à laquelle croît la taille de la surface construite, étape après étape ?
• Quelle peut être la somme des angles d'un triangle ? ...

On pourra comparer avec ce qui ce passe dans le cas d'une surface plate, qui correspond au cas où on recolle seulement k=6 triangles par sommets, et avec le cas où on prend k=5. On peut aussi faire la même construction avec des carrés, en mettant k=3, 4 ou 5 par sommet. On peut modéliser des surfaces bien plus générales en prenant des triangles quelconques, en variant à chaque sommet le nombre de triangles autour...

Un polyèdre convexe, posé sur une surface plane, peut être basculé sur une autre face, par un mouvement de pivot autour d'une de ses arêtes, une culbute.

• Quelles positions peut-on obtenir en enchaînant plusieurs culbutes successives ?
• Par exemple, pour un cube posé sur un échiquier sur la case en bas à droite, peut-on l'amener à la case en bas à gauche de telle manière qu'il soit dans son orientation initiale ?
• On pourra commencer par le tétraèdre régulier, et s'intéresser aux exemples des autres polyèdres réguliers, ou des boites d'allumettes.

Comment faire une carte de la Terre la plus juste possible ?

• On peut par exemple vouloir que les distances représentées sur la carte soient fidèles, ou
• bien que les angles soient justes (par exemple si, en bateau, on souhaite déterminer d'après la carte le cap à suivre pour rentrer au port),
• ou bien que le plus court chemin sur la carte soit bien le plus court chemin dans la réalité...

---