1- Beaucoup de petites choses, ça peut faire combien?
On
construit sur le segment [0, 1] une scie ayant n
= 1, 2,3,... dents
triangulaires de mêmes dimensions et de hauteur commune de
![]() comme sur la figue ci‑dessous
qui illustre le cas n = 4.
comme sur la figue ci‑dessous
qui illustre le cas n = 4.

Que devient la forme de la scie lorsque le nombre de dents devient très très grand ? Qu'en est‑ il de la longueur totale de ses dents (longueur de la ligne brisée) ainsi que de la surface qu'elles délimitent au dessus du segment ?
Étudier le cas où le nombre de dents est n (n = 1, 2, 3, ... ), le cas où la hauteur des dents de la scie est de =2n
Etudier ce problème dans le cas où on a d'autres formes de dents (la courbe qui les délimite n'est pas forcément une ligne brisée) comme le suggère le dessin ci‑dessous.

II‑ Drôles d'opérations.
Pour multiplier 458 par 213, Toto procède comme suit : il dresse d'abord le tableau suivant
|
458 229 114 57 28 14 7 3 1
|
213 426 852 1704 3408 6816 13632 27264 54528
|
puis fait l'addition suivante:
et trouve un résultat! Est‑ce le bon résultat ? Et pourquoi? A vous d'inventer d'autres façons inhabituelles de faire des multiplications, divisions, soustractions!
III‑ En utilisant tous les chiffres de la série 0, 1, 2, 9, les signes arithmétiques.......................................................... x, / et éventuellement
les parenthèses, former un nombre égal à 100.
Exemple: 9 + 81 + 45/(6 + 3) + 7 ‑ 2 + 0 = 100.
Élaborer des principes ou méthodes pour y parvenir.
IV‑ Le mariage des filles de Randomie.
En pays de Randomie on a voulu contrôler la natalité en envisageant de ne pas accorder systématiquement l¹autorisation au mariage; et dès qu'une fille demande l'autorisation de se marier, l'officier d'état civil lui place 6 morceaux de ficelles dans la main. De chaque côté du poing fermé dépassent 6 extrémités. De chaque côté, on choisit au hasard les extrémités par paires et on les noue (figure 1). Si on obtient alors une boucle fermée (figure 2), la fille reçoit l'autorisation de se marier. Sinon, elle recommence l'épreuve un an plus tard.
1
Figure 1. Figure 2.
Angie, qui vient d'avoir 18 ans voudrait se marier. Réussira t‑elle à obtenir l'autorisation de se marier dès la première année?
Et si le nombre de ficelles était n ?
Combien de morceaux de ficelles faut ‑ il prendre pour que seulement 45% des demandes de se marier soient satisfaites.
Quelques années plus tard, Sur le conseil d'un mathématicien et dans l'espoir de réduire la natalité dans le pays on décide que désormais, les extrémités du haut seront nouées avec celles du bas (figure 3). Peut ‑on dire que Tan, une amie d'Angie réussira à se marier ? (le nombre de ficelles peut, ici, être impair).

Figure 3 Figure 4.
Au bout d'un certain temps, on décide de réduire encore la natalité et on décrète (toujours sur le conseil du mathématicien) que chaque extrémité sera attachée au hasard avec une extrémité libre du haut ou du bas (figure 4). Nina, une autre amie d 'Angie sollicite une autorisation au mariage. L'obtiendrait ‑elle?
V‑ Une partie de chasse.
Lors d'une partie de chasse, un chien court derrière un lièvre. Le lièvre court à foulées régulières, toujours à la même vitesse et dans une direction constante. Le chien, un peu à gauche du lièvre, court à la même vitesse que ,celui-ci et infléchissait toujours sa trajectoire de façon à ce que chacune de ses foulées le dirige vers l'extrémité de la dernière foulée du lièvre, comme sur la figure ci-dessous, où L0, L1, ..., L5 (respectivement Ci, C2, .., C5) sont les positions du lièvre (respectivement, du chien) aux instants 0, 1, .... 5&endash;
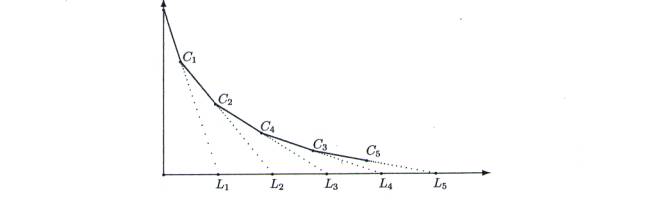
Le chien arrivera t‑ il à rattraper le lièvre ?
Dans le cas négatif, de quelle façon le chien devra t‑il modifier sa stratégie de poursuite (vitesse, position au départ, inflexion de la trajectoire pour qu'il puisse rattraper le lapin? Au bout de combien de temps le rattrapera-t il alors?