|
|
33000 BORDEAUX |
33320 LE TAILLAN MEDOC |
|
|
Pierre GRIHON Agnès GRIMAUD |
Benoît RIVET Joachim BAUDOUIN |
|
|
| |
|
|
Hanna ALLALCHA, Elisabeth GOLOVINA-BENOIS,
Hélène KOVACIC |
Mélodie DURNEZ, Perrine ENJALBERT, Fanny PATIN,
Bénédicte PERES, Aurélie VERDON |
|
|
Le vayageur de commerce /La marche de l'ivrogne | |
Sujet 1 : Problème de billard
[exposé]
nb d'élèves : 3
& 2 (Hanna ALLALCHA, Elisabeth GOLOVINA-BENOIS,
Hélène KOVACIC & Baptiste COUVY, Julien VIGNEAU)
|
La trajectoire d'une boule de billard dépend de la pente de tir initiale :
Pour traiter le sujet, on fera les hypothèhses suivantes :
|
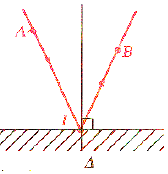 Fig. 1 &endash; Problème du billard. |
Sujet 2 : Evolution d'un population
d'individus. [exposé : Evolution d'un population ]
nb d'élèves :
2 & 7 (Jane MAZOCATTO, Marine TOLEDO & Alicia CAMPOS,
Amélie DANET, Nicolas DEPAS, Emilie HENRY, Marie KOSTUJ,
Florian LEBOEUF, Morgane LUFLADE)
On considère une population d'individus . Celle-ci peut croître ou décroître selon un certains nombres de paramêtres : taux de reproduction, taux de mortalité, ressources limitées en nourriture, en espace, maladies,...
- Comment évolue cette population au
fil des années ?
Pour traiter le sujet, on envisagera chacun des cas suivants :
1er cas : La croissance ou la décroissance de la population ne dépend que d'un seul paramêtre : le taux de "croissance"
2ème cas : La croissance ou la décroissance de la population dépend de deux paramêtres : le taux de croissance et une certaine limitation des ressources (le nombre d'individus ne peut dépasser une population " limite " ).
Sujet 3 : Le voyageur de commerce
[atelier]
nb d'élèves : 0 &
3 (Julien BERNARD, Adèle DROUET, Cécile
VOINIER)
M. Pierre est voyageur de commerce. Il fait la tournée des petits commerces de la région Aquitaine pour vendre des pots de manchons de canard de la marque «Lacassagne». Cela fait beaucoup de démarchage, la route est longue, et il souhaite quitter sa famille le moins longtemps possible.
- Son problème est simple : ayant fait la liste de tous les commerces à visiter, ayant repéré sur la carte les routes d'Aquitaine ainsi que la localisation des commerces, comment définir un trajet permettant de ne passer qu'une fois, ou le moins de fois possible, devant chaque commerce ?
Sujet 4 : Un ivrogne a-t-il une chance
d'arriver en un lieu donné ? [exposé :
La marche de
l'ivrogne]
nb d'élèves : 6 & 5 ( Baudoin AUZOU,
Guillaume CAMELOT, Antoine CAROF, Luc DARNE, Alice DESIDERI, Camille
LACAULE & Mélodie DURNEZ, Perrine ENJALBERT, Fanny PATIN,
Bénédicte PERES, Aurélie VERDON )
|
A la fin d'une soirée bien trop arrosée, M. Pierre, toujours lui1, sort du restaurant dans un état qui ne lui permet pas de se déplacer de manière déterministe. Autrement dit, il voit des éléphants roses à tous les carrefours ou presque. Cependant, le monde est bien fait : M. Pierre ne peut se déplacer que suivant un réseau cartésien, mais il le fait de manière aléatoire. Une fois sur quatre, il se choisit de se déplacer vers le nord ou vers le sud, ou vers l'ouest, on encore au sud. M. Pierre doit retrouver un endroit donné : soit sa chambre, soit un bistrot, ou encore le restaurant où il a égaré son porte&endash;monnaie. |
 Fig. 2 &endash; Les pérégrinations de M. Pierre. |
- Monsieur Pierre trouvera&endash;t&endash;il cet endroit à coup sûr ?
- Ou a&endash;t&endash;il une bonne espérance de le faire ?
- On peut aussi faire le même problème en supposant qu'il se déplace sur une droite (mais avec une probabilité 1/2 d'aller vers la roite ou vers la gauche),
- ou encore qu'il est capable de voler et de se déplacer dans l'espace (avec une probabilité 1/6 par direction possible).