Sujets du Club Math en Jeans du Lycée Blaise Pascal à Orsay pour 2004-2005

1 Les prisonniers

Quarante savants sont faits prisonniers par un dangereux concurrent jaloux qui les réunit dans une salle et les met en garde : "Vous allez être emprisonnés dans des cellules individuelles complètement fermées, desquelles vous ne verrez ni n'entendrez rien. Toutes les heures, nous choisirons l'un d'entre vous au hasard et nous le guiderons dans une petite salle où il pourra manger et boire. Votre seul moyen de communiquer sera d'éteindre ou d'allumer la lampe de la salle. Cela ne finira jamais, sauf si l'un d'entre vous, un jour, nous demande d'arrêter. Ce jour là sera décisif : si, à cet instant, vous avez tous mangé au moins une fois, vous serez libérés. Sinon, je vous exécuterai sur le champ. Je vous laisse une heure pour en discuter. Ensuite, mes hommes vous conduiront dans vos cellules." Et il quitte la pièce. Que peuvent bien se dire les savants ?

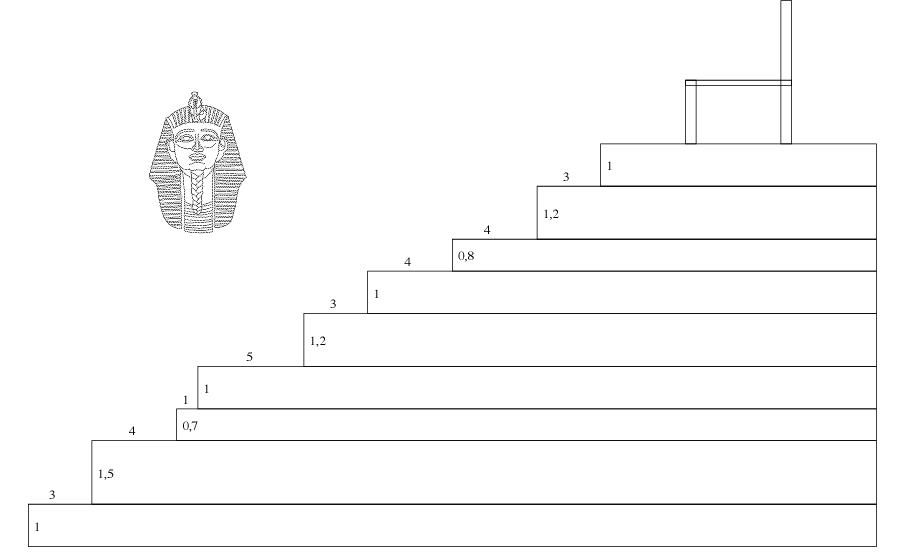
2 L'escalier du Pharaon

Dans l'Egypte ancienne, le vieux pharaon s'était fait construire un escalier en or d'un mètre de large dont le plan est reproduit ici (les longueurs sont en décimètres). Comme il était très fatigué, il avait demandé à ses architectes de lui faire des marches très basses.

Mais, quand il mourut, son jeune fils pensa qu'un escalier à marches hautes impressionnerait bien plus ses visiteurs. Il demanda donc à son architecte de le combler pour faire en sorte qu'il ne reste que quatre marches. Celui-ci revint le lendemain avec un plan, et annonça à son Pharaon qu'il avait besoin de 345 dm ³ d'or. Le Pharaon, que les guerres avaient presque ruinées, ne disposait que de 200 dm ³ d'or. Courroucé, il menaça son architecte de le faire jeter aux crocodiles s'il n'arrivait pas à se débrouiller avec. Mais, dans son infinie bonté, il lui promit le complément si l'architecte se débrouillait avec moins d'or que cela.

A la place de l'architecte, sauriez-vous sauver votre peau, ou peut-être même assurer votre richesse ?

3 Le manuscrit de Saragosse

A la mort du chef de famille, ses deux enfants découvrirent un manuscrit qui les rendit perplexes : "J'ai laissé sur un compte rapportant 20% d'intérêts annuels les 100.000 réaux que j'ai pu économiser au cours de ma longue vie. Cette somme n'est pas pour vous : je la destine aux pauvres de la ville qui en ont plus besoin. Mais je sais que vous avez besoin d'aide pour vous installer, aussi vous laissé-je pendant 10 ans gérer les intérêts qu'elle rapporte : chaque fin d'année, vous pouvez en retirer la somme que vous voulez, et laisser le reste capitaliser avec la somme initiale à laquelle vous ne pourrez pas toucher. Arrangez-vous comme bon vous semble, mais n'oubliez pas qu'au terme de cette période, tout ce qui restera sur le compte sera pour les nécessiteux !" Beaucoup moins généreux que leur père, les deux fils entrèrent immédiatement dans une grande colère d'être ainsi déshérités. Puis ils durent se mettre d'accord pour la gestion des intérêts. Mais comment doivent-ils s'y prendre pour retirer un maximum d'argent de la situation ?

4 La fête des schtroumphs

Aujourd'hui les schtroumphs font une fête ; pour l'occasion, ils vont changer de chapeaux, pour que la farandole soit plus belle. Aussi passent-ils tour à tour dans la maison des chapeaux, grand champignons où de nombreux chapeaux jaunes et violet sont entreposés et dans lequel l'électricité n'a pas encore été installée. Chaque schtroumph ressort ainsi chapeauté d'un bonnet dont il ne connaît pas la couleur. Une fois chacun coiffé, on observe les schtroumphs s'agiter en tout sens... A l'issue de cette manœuvre, tous les chapeaux violet sont séparés des chapeaux jaunes, SANS QU'ILS AIENT JAMAIS COMMUNIQUÉ ENTRE EUX. Comment ont-ils fait ?

5 Imitons nos voisins

On dispose d'un échiquier n * n ; on place un nombre réel sur chaque case de son bord.

Est-il possible de mettre, sur chaque case, un réel de sorte qu'il soit la moyenne des 4 nombres voisins ?

6 Là où se trouve le trésor ?

On trouve souvent chez les antiquaires toutes sortes de cartes. L'autre jour que je furetai chez l'un d'entre eux, je tombai sur deux cartes d'une même île, l'une de 1 mètre sur 1 mètre et l'autre, parfaite copie de la première, de 20 cm sur 20 cm, mises l'une sur l'autre comme sur le dessin : ... Chose extraordinaire, il y avait un point où les deux cartes se superposaient ! Après un moment de réflexion, je trouvai cela normal... Mais quelle ne fut pas ma surprise lorsque je jetai sur la grande carte une vieille carte toute déformée de cette même île : il y avait toujours un point où les deux cartes figuraient le même endroit. Je restai pensif... Pourrez-vous m'aider ?

7 Le désert des dunes

On considère un désert, composé de dunes numérotées de 1 à n, et d'un trou (sans fond) T. La i-ème dune est voisine de d_i autres dunes, avec i compris entre 1 et n, et peut être voisine du trou, ou pas.
Chaque dune est composée, à l'instant initial, de n_i grains de sable.
Un éboulement sur la i-ème dune enlève, lorsque c'est possible, d_i + 1 grains de sable de la dune si elle est voisine du trou T, et d_i grains sinon, et rajoute un grain de sable sur chacune des dunes voisines. On dit que le désert est stable s'il n'y a d'éboulement possible sur aucune dune.

Le désert peut-il devenir stable ?

8 Le tournesol artilleur

Pour placer des graines dans sa fleur, un tournesol circulaire procède ainsi : Un canon à graines placé en son centre envoie une première graine dans une certaine direction. Elle va tout droit, et s'arrête au bord de la fleur (1). Puis le canon tourne d'un angle a, puis envoie une seconde graine. Celle-ci s'arrête dès qu'elle touche soit une autre graine déjà placée, soit le bord. etc. La nature ayant horreur du vide, comment a-t-elle choisi l'angle a ? Regardez de près une fleur de tournesol [image 190 Ko]