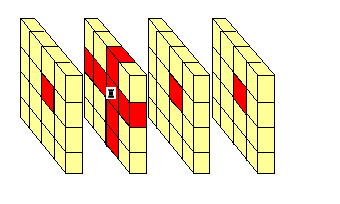
L'échiquier 4 x 4 x 4 avec une tour et les cases qu 'elle contrôle
(on a éclaté l'échiquier en plateaux séparés pour mieux voir).
|
|
95 St BRICE (Classe de 4ème optionelle à projet scientifique) |
95 MONTMORENCY |
|
|
M. Eric MARTINOD |
M. Christian GEORGES |
|
|
| |
|
|
| |
Sujet 1
: Les tours sur l'échiquier
3D. [exposé]
(sujet du "LaboraToile" )
nb d'élèves : 7 &
4
L'échiquier à trois dimensions est un cube partagé en n x n x n cases, chacun des côtés étant divisé en n intervalles égaux. Une "tour" contrôle les trois lignes de cases parallèles aux côtés passant par la case où elle se trouve.

On se demande :
- Combien au maximum peut-on placer de tours, et comment peut-on les placer, de façon qu'aucune d'elles n'en menace une autre ?
- Combien au minimum faut-il en placer, et comment, de façon qu'ensemble elles contrôlent toutes les cases de l'échiquier.
Sujet 2 :
Des carrés dans les
rectangles. [exposé]
nb d'élèves :
6 & 4
Un rectangle a deux dimensions, disons sa largeur et sa hauteur et la proportion largeur/hauteur donne la forme du rectangle. Par exemple, un écran 16/9 est un écran rectangulaire dont la proportion largeur/hauteur est égale à 16/9. Ces écrans peuvent être grands ou petits, mais ils ont tous la même forme. A tout nombre positif correspond une forme de rectangles.
Si vous cherchez à quel nombre correspond un rectangle, vous pouvez bien sûr mesurer sa largeur et sa hauteur avec la règle et faire la division, mais ce n'est pas une méthode exacte. Voici une méthode géométrique :
En reportant la largeur sur la hauteur si elle est plus grande (en pliant ou avec le compas), et le contraire sinon, on divise le rectangle en un carré et un rectangle plus petit. On regarde ce nouveau rectangle et on recommenceŠ. Par exemple avec un rectangle de 16 x 9, cela donne le dessin suivant
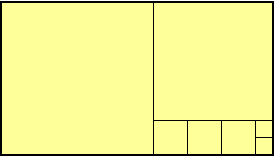
Le découpage comprend successivement 1 carré pris dans la largeur, 1 dans la hauteur, 3 dans la largeur, 2 dans la hauteur puis on s'arrête puisqu'il ne reste plus rien. On code alors 1-1-3-2.
Faites le découpage avec d'autres rectangles. Essayez avec des rectangles tracés sur un quadrillage pour aller plus vite et pour avoir des figures exactes - vérifiez en calculant les dimensions des carrés et des rectangles successifs. Essayez aussi avec une feuille de papier A4 standard, de dimensions approximatives 210 et 297mm.
Questions :
&endash; Comment retrouver les proportions des rectangles à partir de leurs codages ?
&endash; Si on part de n'importe quelle forme, est-on sûr que le découpage s'arrête ?
&endash; Comment comparer deux nombres si je connais leurs codages ?
Maintenant, la feuille de papier A4 ne fait pas exactement 210mm x 297mm. La proportion exacte (hauteur/largeur) est racine de 2 (noté ˆ2) qui est aussi le rapport de la diagonale du carré à son côté. On peut expliquer pourquoi elle a été choisie comme ça, mais si vous voulez le vérifier, reportez la largeur sur la hauteur comme dans le découpage et vérifiez que la diagonale du carré est bien égale à la hauteur de la feuille.
A votre avis, quel codage va-t-on trouver ? Si vous avez une idée, pouvez-vous montrer qu'elle est juste ?
Ensuite, pouvez-vous utiliser ce codage pour comparer ˆ2 et 297/210 ? pour trouver d'autres fractions approchant mieux ˆ2 ? pour trouver la valeur de ˆ2 plus précisément que ce que vous obtenez avec votre calculatrice ?
Sujet 3
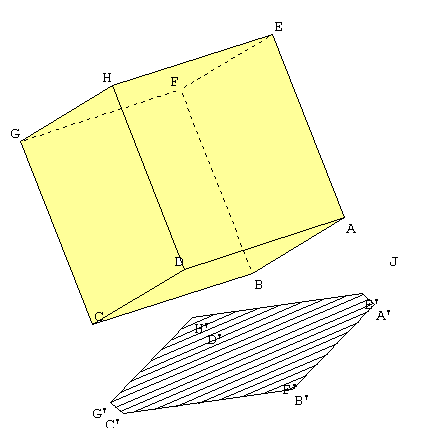
: L'ombre d'un cube.
[exposé]
nb d'élèves : 4+4 &
0
|
L'ombre d'un cube peut-elle être un triangle ? un quadrilatère ? un quadrilatère quelconque ? un pentagone ? un hexagone régulier ? un hexagone quelconque ?
|
|
Sujet 4
: Touche à tout ?
[exposé]
nb d'élèves : 7 & 4
Au rugby, il y a deux manières de jouer une touche :
- La première consiste à aligner les
deux équipes face au lanceur. Celui qui saute le plus haut
prend la balle.
- Depuis peu un joueur peut jouer la touche rapidement sans attendre
que les équipes se mettent en place ; à condition de
l'envoyer à un joueur se trouvant à plus de 5
mètres du bord du terrain.
- Si aucun joueur n'est assez près de lui, il peut se
l'envoyer à lui-même à condition de courir les 5
mètres pour la rattraper.