Avec quatre triangles, par exemple, on peut fabriquer un tétraèdre (pyramide à base triangulaire). Plus généralement on peut fabriquer certains polyèdres, appelés deltaèdres (à cause de la forme de la lettre grecque "delta" : )]: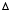

• Mais au fait, qu'est-ce qu'un polyèdre ?

Admettons maintenant qu'on sache ce qu'est un polyèdre (cube, octaèdre, étoile ...). Un deltaèdre est un polyèdre dont toutes le faces sont des triangles équilatéraux.

• Recherche de méthodes pour fabriquer des deltaèdres spectaculaires (par pliage par exemple, ou avec des tiges de bois), ou d'autres formes à base de riangles équilatéraux
  Exemple 1. Réalisation d'un endo-pentakis-icosi-dodécaèdre par pliage circulaire :
  Exemple 2. Tressage de deltaèdres.
  Qu'est-ce qu'un tressage ? Ci dessous, on donne deux découpages permettant de tresser à gauche, un cube, à droite un icosaèdre
                                                        
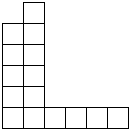
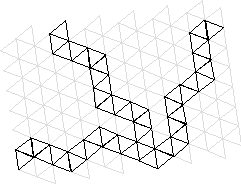
  Chercher des découpages permettant de fabriquer certains deltaèdres par tressage. Est-ce toujours possible ? Les modèles seront dessinés à l'aide d'un logiciel de dessin et devront être effectivement réalisés.
  
• Problèmes d'existence : étudier les nombres de faces, d'arêtes, de sommets des deltaèdres. Peut-on fabriquer des deltaèdres avec cinq triangles équilatéraux, six, sept, etc . et jusqu'à combien ? Peut-on continuer indéfiniment ? Pensez vous que la géode (à la cité des sciences et de l'industrie à Paris), par exemple, soit fabriquée avec des triangles équilatéraux ?
  
• Chercher à les dénombrer : combien y-a-t-il de deltaèdres à 4 faces, 5 faces, Š10 faces, Š
• Y a-t-il une, ou des relations entre les nombres de faces, d'arêtes, de sommets ? Que se passe-t-il si l'on impose des règles du type : trois faces par sommet, quatre faces par sommet, cinq faces par sommet, six, sept . peut-on classer les polyèdres qu'on a trouvés, et comment ?
• Quels sont les deltaèdres convexes et pourquoi ... ?
• Est-ce qu'on obtiendra toujours des polyèdres rigides ?
• Si l'on autorise les polyèdres à présenter un trou (comme une bouée) ou deux (comme un huit), ou plus, qu'est-ce qui change ?
• Essayer de fabriquer une surface fermée sans dessus ni dessous (comme la bouteille de Klein) avec des triangles équilatéraux.

Sujet n°2a : Coloriage des deltaèdres. Nb. d'élèves : 6 & 3

• Comment, avec le moins possible de couleurs, colorer les faces de manière à ce que deux faces adjacentes recoivent des couleurs différentes.
• Chercher des règles ; les démontrer. Peut on colorier un deltaèdre dont tous les sommets ont le même nombre de faces, (3, 4, 5..), avec 3, 4, 5 couleurs selon le cas, de telle façon que chaque sommet possède n couleurs exactement et que deux faces adjacentes soient toujours différentes. Si oui, de combien de façons distinctes ?

Sujet n°2b : Deltaèdres convexes. [Exposé]
Nb. d'élèves : 4 & 0

• Quels sont les deltaèdres convexes et pourquoi ...

Sujet n°2c : Polypolyèdres. [Exposé]
Nb. d'élèves : 3 & 3

Voici un exemple. Premier: challenge : comment le fabriquer ?

Sujet n°2d : Deltaèdres de Möbius [Exposition sur stand]
Nb. d'élèves : 0 & 2

Voici un « delatèdre de Möbius :

nous le fabriquerons avec des « fonds de tarte, ainsi que d'autres ayant des propriétés similaires.

Sujet n°2e : Polyèdres flexibles [Exposé]
Nb. d'élèves : 0 & 1

Ils se déforment bien que leur faces restent rigides.