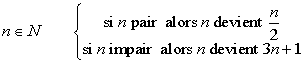
Etablissements |
Lycée Sud Médoc |
Lycée Montaigne |
Professeurs |
Mme Dominique Grihon |
M. Olivier Carcone |
Chercheur |
M. Laurent Habsieger (Université Bordeaux I) |
|
Sujet 1 : Problème de syracuse. (photos)
On considère la transformation définie sur les entiers par :
On réitère ce processus, retrouve-t-on toujours la valeur 1 ?
Sujet 2 : Chaines d'additions. (photos)
Une chaine d'additions est une suite d'entiers commençant par 1, telle que chaque terme supplémentaire est obtenu en additionnant deux des termes qui précèdent. La longueur d'une chaine d'additions est le nombre de ses termes. Une chaine d'additions pour nest une chaine qui se termine par n. On note l( n) la longueur minimale d'une chaine d'additions pour n. Etudier la conjecture de Scholz qui énonce que :
Sujet 3 : Fractions egyptiennes. (photos)
Une fraction égyptienne est une fraction de la forme 1/m, où m est un entier naturel. La conjecture D'Erdös-Straus affirme que toute fraction de la forme 4/n peut être décomposée en somme de trois fractions égyptiennes.
A-t-on toujours
?
La conjecture de Sierpinski est similaire et concerne la décomposition de 5/n en trois factions égyptiennes.
Sujet 4 : Loto sportif. (photos)
Une grille de loto sportif comporte 13 lignes et trois colones. On coche 1 case dans chaque ligne et on compare à la grille des résultats. On gagne si on a commis moins de trois erreurs.
Nombre minimal de grilles à remplir pour être sûr de gagner quels que soient les résultats ?