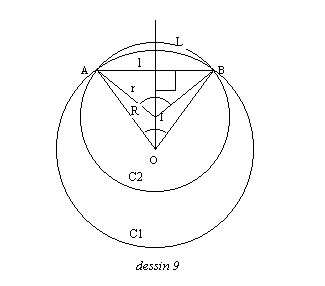
Dans le triangle ABI, on a : b = angle AIB
et AI = r
donc ![]()
De même dans le triangle OBA, on a : ![]()
avec a = angleAOB
Ainsi : ![]() et
et ![]() .
.
Preuve :
|
Dans le triangle ABI, on a : b = angle AIB et AI = r donc De même dans le triangle OBA, on a : avec a = angleAOB Ainsi :
|
 |
On sait que dans un cercle de rayon R la longueur L de l'arc de mesure a est R a
Etudions le signe de L - l :
L - l = b r - a
R est du même signe que ![]()
et donc du même signe que ![]()
Or ![]() d'où
d'où
![]()
On pose a =![]() et f(x) = sin (ax) – a sin x
et f(x) = sin (ax) – a sin x
Etudions les variations de la fonction f sur
![]()
f’(x) = a cos (ax) – a cos x
f’(x) = a (cos (ax) – cos x)
On a 0 £ ax
£ x £ ![]() donc l'expression( cos (ax) – cos(x)) est positive car la fonction "cos"
est décroissante sur
donc l'expression( cos (ax) – cos(x)) est positive car la fonction "cos"
est décroissante sur ![]()
f'(x) étant positif sur l'intervalle![]() f est croissante sur
f est croissante sur ![]()
De plus, f(0) = 0, donc f(x) est toujours positive sur ![]()
Donc L – l ne peut être nul que si a et b sont nuls, L - l est strictement positif
Conclusion :
L’arc AB du cercle C1 est plus court que l’arc AB du cercle C2
Cela justifie qu'on appelle distance AB entre 2 points de la sphère la longueur de l'arc de géodésique passant par ces points.