Comptes Rendus MATh.enJEANS,
04-04
Le
problème du cavalier
par
Arnaud DUMAS, Antony
LEE, Gaël
LEMOINE,
Régis
MILLET, Nelle
VAROQUEUX, Catherine
WACOGNE
élèves
du lycée Blaise Pascal
(Orsay)
(Texte de Antony
LEE)
Club Math en Jeans du Lycée Blaise
Pascal
(Orsay &endash; Essonne). Atelier scientifique année
2003-2004.
Professeurs
:
Chantal BASTIN, Nadine DELBARRE, Denis JULIOT, Didier
MISSENARD
Chercheurs
:
Cédric BOUTILLIER, Aurélien GARIVIER
(Moniteurs Université Paris Sud, Orsay), Pierre PANSU
(Université Paris Sud, Orsay ), Frédéric PAULIN
(ENS),
 [Article en cours d'analyse
et de vérification : les passages entre crochets sont des
éditeurs]
version pdf de l'article [2,7
Mo]
[Article en cours d'analyse
et de vérification : les passages entre crochets sont des
éditeurs]
version pdf de l'article [2,7
Mo]
[Sujet initial de Pierre PANSU]
- Sur la demi-droite des naturels, si l'on se donne deux entiers
p et q, peut-on, en partant de l'origine, atteindre tout point du
segment [0 ; N] en ne se déplaçant que de p ou q pas
dans une direction ou l'autre ?
- Dans le plan discret, si l'on se donne un carré N *N,
peut-on, par des déplacements de cavaliers d'ampleur p et
q, atteindre tout point du carré ?
- Dans l'espace discret, si l'on se donne un cube N *N *N,
peut-on, par des déplacements de cavaliers d'ampleur p, q,
r atteindre tout point du cube ?
I.
Le problème
Un cavalier se déplace le long dčune bande, divisée
en cases numérotées par les entiers naturels,
n étant le numéro attribué la
nième case en partant de lčorigine. Le
cavalier peut se déplacer soit de
p cases, soit de
q cases
(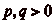 ), en avant ou en
arrière. On place sur cette demi-droite un mur, auquel
correspond le numéro m (
), en avant ou en
arrière. On place sur cette demi-droite un mur, auquel
correspond le numéro m (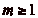 ), qui empêche le cavalier de passer
par une quelconque case dont le numéro est strictement
supérieur à celui du mur.
), qui empêche le cavalier de passer
par une quelconque case dont le numéro est strictement
supérieur à celui du mur.
On demande si lčon peut placer le mur de manière à
ce que le cavalier, en partant de la case 0, puisse atteindre toutes
les cases situées entre la case 0 et la case
m (au sens large), et, si cela
est possible, quelles valeurs peut on donner à
m.
II.
Condition nécessaire pour
lčexistence de m.
On exclut le cas où 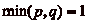 , où
on a trivialement
, où
on a trivialement 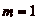
Il est évident que toutes les cases pouvant être
atteintes par le cavalier ont un numéro qui peut
sčécrire sous la forme 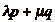 (
(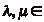 Z), donc
divisible par
Z), donc
divisible par 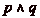 . On doit
donc avoir, si lčon veut atteindre toutes les cases,
. On doit
donc avoir, si lčon veut atteindre toutes les cases,
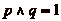 .
.
On supposera donc que 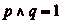 et que
et que
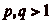 dans la suite de
lčexposé.
dans la suite de
lčexposé.
III.
Existence de m sous
la condition précédente.
Montrons que  convient.
convient.
On va commencer par montrer que pour tout 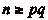 , il existe
, il existe
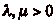 tels que
tels que
 .
.
En effet, dčaprès le théorème de
Bézout, il existe 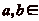 Z tels que
Z tels que
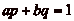 , soit, pour tout
, soit, pour tout 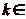 Z,
Z,
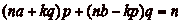 .
.
Or, pour que 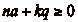 et
et 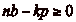 , il faut et suffit que
, il faut et suffit que  . Or, il
existe toujours un entier dans lčintervalle
. Or, il
existe toujours un entier dans lčintervalle
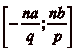 , puisqučil est dčamplitude
, puisqučil est dčamplitude
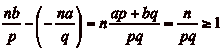 .
.
CQFD.
Pour tout 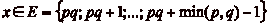 , il existe donc
, il existe donc
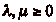 tels que
tels que 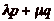 , et la case
x peut donc être atteinte par le
cavalier qui, en faisant
, et la case
x peut donc être atteinte par le
cavalier qui, en faisant 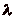 pas de p cases en avant et
pas de p cases en avant et
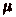 pas de
q cases en avant,
arrive sur la case souhaitée en passant par des cases de
numéros croissants, et donc ne dépasse pas le mur, dont
le numéro est supérieur ou égal à celui
de la case que lčon souhaite atteindre.
pas de
q cases en avant,
arrive sur la case souhaitée en passant par des cases de
numéros croissants, et donc ne dépasse pas le mur, dont
le numéro est supérieur ou égal à celui
de la case que lčon souhaite atteindre.
Dčautre part, soit 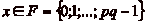 ,
, 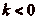 le quotient et
le quotient et  le reste
de la division euclidienne de
le reste
de la division euclidienne de 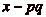 par
par  . On a
. On a
 ,
dčoù
,
dčoù
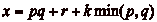 . On a
. On a 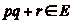 , donc
, donc 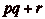 est atteignable. On peut donc
atteindre la case x en se
rendant dčabord sur la case
est atteignable. On peut donc
atteindre la case x en se
rendant dčabord sur la case 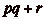 , puis en reculant de
, puis en reculant de
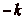 fois de
fois de 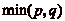 , et ce
quelque soit
, et ce
quelque soit 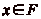 . Comme on
peut aussi atteindre les cases de
E,
. Comme on
peut aussi atteindre les cases de
E,  convient
donc (puisque
convient
donc (puisque 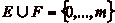 ).
m existe donc. CQFD.
).
m existe donc. CQFD.
IV.
Ensemble des valeurs pouvant être
prises par m.
Soit m1 une valeur possible de
m. Montrons que tout m'>
m1 est
également une valeur possible de
m.
En effet, on a clairement  (puisque pour atteindre toutes les cases de
(puisque pour atteindre toutes les cases de
 , il faut faire au moins un
déplacement).
, il faut faire au moins un
déplacement).
Soit 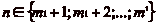 et
r le reste de la division euclidienne de n par
et
r le reste de la division euclidienne de n par
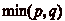 .
. 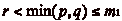 , donc la
case r est atteignable sans dépasser
le mur placé en mč. Pour atteindre la case
n sans dépasser ce même
mur, il suffit dčaller en r, puis dčavancer du bon nombre de fois
de
, donc la
case r est atteignable sans dépasser
le mur placé en mč. Pour atteindre la case
n sans dépasser ce même
mur, il suffit dčaller en r, puis dčavancer du bon nombre de fois
de 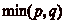 cases.
CQFD.
cases.
CQFD.
Ainsi, pour déterminer lčensemble des valeurs pouvant
être prises par m, il suffit de déterminer le plus petit
élément de cet ensemble. Lčensemble recherché
sera alors composé de tous les entiers supérieurs ou
égaux à ce plus petit élément.
V.
Plus petite valeur pouvant être prise
par m.
On va montrer que cette plus petite valeur est 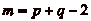 .
.
a.
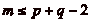
Montrons que toutes les cases peuvent être atteintes avec un
mur placé à 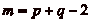 .
.
Pour cela, commençons par remarquer que si lčon peut
atteindre toutes les cases de 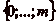 en partant de la case 0, on peut aussi le
faire en partant de nčimporte quelle case de
en partant de la case 0, on peut aussi le
faire en partant de nčimporte quelle case de
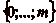 . En effet, il suffit pour cela de se rendre
de la case de départ à la case 0 (en suivant le chemin
inverse de celui que le cavalier suit pour aller de la case 0
à la case de départ), à partir de laquelle il
est possible de se rendre sur nčimporte quelle case de
. En effet, il suffit pour cela de se rendre
de la case de départ à la case 0 (en suivant le chemin
inverse de celui que le cavalier suit pour aller de la case 0
à la case de départ), à partir de laquelle il
est possible de se rendre sur nčimporte quelle case de
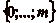 (par hypothèse).
(par hypothèse).
Le mur étant placé en 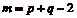 , demandons au cavalier,
initialement placé sur la case
, demandons au cavalier,
initialement placé sur la case
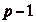 , de réaliser le parcours
suivant : sčil peut reculer de q cases ou avancer de p cases, il le fait (les deux ne sont
pas possibles simultanément, puisque la longueur de segment
qučil peut parcourir est de
, de réaliser le parcours
suivant : sčil peut reculer de q cases ou avancer de p cases, il le fait (les deux ne sont
pas possibles simultanément, puisque la longueur de segment
qučil peut parcourir est de 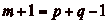 cases),
sinon il sčarrête.
cases),
sinon il sčarrête.
En notant xn le numéro de la case
où se trouve le cavalier après le
nième
déplacement (x0 étant par convention la
case de départ du cavalier), on a donc :
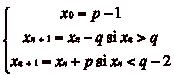
Si 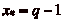 , le cavalier sčarrête.
, le cavalier sčarrête.
Nous allons montrer qučen suivant un tel parcours, le cavalier
passe nécessairement une unique fois par toutes les cases de
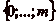 , et
seulement celles-ci.
, et
seulement celles-ci.
Il est clair que par construction, la suite 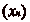 est
à valeurs dans
est
à valeurs dans 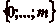 , et que
pour tout n pour lequel
, et que
pour tout n pour lequel
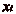 est défini, il existe
est défini, il existe
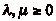 tels que
tels que 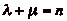 et
et
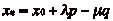 , le cavalier ne faisant que
des déplacements de
p cases en avant et des
déplacements de
q cases en
arrière.
, le cavalier ne faisant que
des déplacements de
p cases en avant et des
déplacements de
q cases en
arrière.
Montrons, par lčabsurde, que cette suite ne boucle pas. Supposons
que la suite boucle, cčest à dire qučelle est
périodique à partir dčun certain rang. Dans ce cas, il
existe 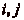 (
(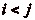 ) distincts tels que
) distincts tels que
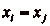 et que
et que 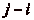 soit
minimum. Alors la suite prend des valeurs deux à deux
distinctes pour des indices compris (au sens large) entre
i et
soit
minimum. Alors la suite prend des valeurs deux à deux
distinctes pour des indices compris (au sens large) entre
i et
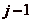 , par hypothèse de
minimalité sur
, par hypothèse de
minimalité sur 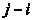 . Comme la
suite est à valeurs dans
. Comme la
suite est à valeurs dans 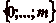 , on a donc
, on a donc 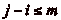 (
( est lčensemble des valeurs que peut prendre
la suite, au nombre de m ; or, entre
xi et
est lčensemble des valeurs que peut prendre
la suite, au nombre de m ; or, entre
xi et
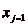 , la suite prend par hypothèse des
valeurs deux à deux distinctes, au nombre de
, la suite prend par hypothèse des
valeurs deux à deux distinctes, au nombre de 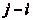 ).
).
Il existe donc 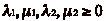 tels que
tels que
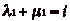 et
et 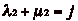 , ainsi que
, ainsi que
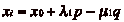 et
et
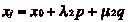 , soit
, soit
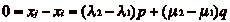 , dčoù
, dčoù
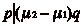 et
et
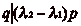 . On a aussi
. On a aussi 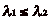 et
et
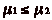 , puisque
, puisque
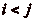 . p et q
étant supposés premiers entre eux, dčaprès le
théorème de Gauss, on a
. p et q
étant supposés premiers entre eux, dčaprès le
théorème de Gauss, on a 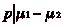 et
et
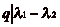 . Dčautre part, si
. Dčautre part, si 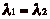 , alors
lčégalité
, alors
lčégalité 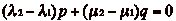 entraîne clairement
entraîne clairement 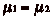 , soit
, soit
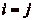 , ce qui est exclu par
hypothèse. Donc
, ce qui est exclu par
hypothèse. Donc 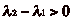 , et, de même,
, et, de même, 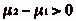 . On a donc
. On a donc
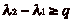 et
et
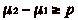 , dčoù
, dčoù
 , ce qui est absurde.
, ce qui est absurde.
Ainsi, pour tout 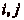 (
( ) pour lesquels la suite est définie,
) pour lesquels la suite est définie,
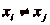 . Or, la suite ne peut prendre que
. Or, la suite ne peut prendre que
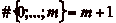 valeurs distinctes, ce qui signifie que la
suite ne sera jamais définie pour des indices
supérieurs ou égaux à
m. Puisque si
valeurs distinctes, ce qui signifie que la
suite ne sera jamais définie pour des indices
supérieurs ou égaux à
m. Puisque si
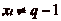 ,
, 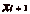 est défini, on en déduit
qučil existe k tel que
est défini, on en déduit
qučil existe k tel que 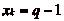 . Il existe donc
. Il existe donc 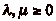 tels que
tels que
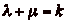 et
et
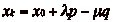 , dčoù
, dčoù
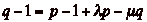 , soit
, soit
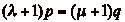 , dčoù, p et q
étant premiers entre eux,
, dčoù, p et q
étant premiers entre eux,
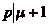 et
et 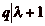 , dčoù
, dčoù
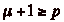 et
et
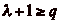 , et
, et
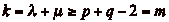 .
.
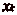 étant par hypothèse
défini, on en déduit
étant par hypothèse
défini, on en déduit
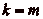 (puisque
(puisque
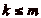 ).
).
Donc ce parcours va faire passer le cavalier par les cases
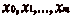 , cčest à dire par
, cčest à dire par 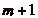 cases deux
à deux distinctes. Comme lčon demande au cavalier de passer
par les
cases deux
à deux distinctes. Comme lčon demande au cavalier de passer
par les 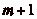 cases
cases
 , on en déduit que le
cavalier va effectivement passer par toutes les cases
souhaitées. CQFD.
, on en déduit que le
cavalier va effectivement passer par toutes les cases
souhaitées. CQFD.
b.
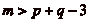
Montrons qučun mur placé à
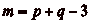 ne permet pas au cavalier de
passer par toutes les cases. Supposons, par symétrie des
rôles, que
ne permet pas au cavalier de
passer par toutes les cases. Supposons, par symétrie des
rôles, que 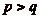 . On
commence par exclure le cas où
. On
commence par exclure le cas où
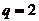 . Dans ce cas, si
. Dans ce cas, si 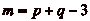 , on aurait
, on aurait
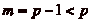 , cčest à dire que le
cavalier nčaurait pu faire que des déplacements de
, cčest à dire que le
cavalier nčaurait pu faire que des déplacements de
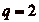 cases, puisque tout déplacement de
p cases le ferait
dépasser les limites. Le cavalier ne pourrait donc pas
atteindre les cases de numéro impair, ce qui conclut la
démonstration.
cases, puisque tout déplacement de
p cases le ferait
dépasser les limites. Le cavalier ne pourrait donc pas
atteindre les cases de numéro impair, ce qui conclut la
démonstration.
Nous allons introduire la notion de classe de congruence modulo
q. La classe de congruence de
a modulo
q est lčensemble des entiers congrus
à a modulo
q, cčest à dire
sčécrivant sous la forme 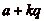 (
( ). Dans ce qui suit, on sous-entendra le
« de congruence modulo q ».
). Dans ce qui suit, on sous-entendra le
« de congruence modulo q ».
Montrons qučil existe exactement q classes : celle de 0 (lčensemble des
multiples de p), celle de 1,, celle de
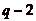 et celle de
et celle de 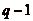 .
Dčaprès la définition, la différence de deux
entiers dčune même classe est divisible par q, puisqučon a
.
Dčaprès la définition, la différence de deux
entiers dčune même classe est divisible par q, puisqučon a
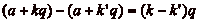 , que divise
q. Comme la
différence de deux entiers distincts de
, que divise
q. Comme la
différence de deux entiers distincts de
 appartient clairement à
appartient clairement à
 , elle ne peut être divisible par
q, et les classes de 0,
1,..,
, elle ne peut être divisible par
q, et les classes de 0,
1,..,  sont donc distinctes. En revanche, tout
entier nčappartenant pas à
sont donc distinctes. En revanche, tout
entier nčappartenant pas à 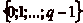 appartient
clairement à la classe du reste de sa division euclidienne par
q.
appartient
clairement à la classe du reste de sa division euclidienne par
q.
Il sčensuit que les q classes que sont celle de 0, celle de 1,, celle de
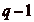 sont deux
à deux distinctes, et que ce sont les seules. Il existe donc
q classes.
sont deux
à deux distinctes, et que ce sont les seules. Il existe donc
q classes.
Dčautre part, les classes de 0, p,,
 sont deux à deux distinctes, car si
kp et
sont deux à deux distinctes, car si
kp et
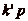 étaient dans la même classe
(avec
étaient dans la même classe
(avec 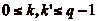 et
et
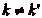 ), alors
), alors
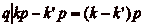 , dčoù, p et
q étant premiers
entre eux, dčaprès le théorème de Gauss,
, dčoù, p et
q étant premiers
entre eux, dčaprès le théorème de Gauss,
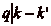 . Comme la différence de
deux entiers distincts de
. Comme la différence de
deux entiers distincts de  appartient clairement à
appartient clairement à
 , elle ne peut être divisible par
q, kp et
, elle ne peut être divisible par
q, kp et
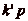 sont dans des classes distinctes.
sont dans des classes distinctes.
Lčensemble des q classes
que sont celle de 0, celle de p,, celle de 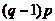 est donc égal à lčensemble de
toutes les classes.
est donc égal à lčensemble de
toutes les classes.
La démonstration suivante repose sur le dénombrement
des classes que le cavalier peut atteindre. Nous allons montrer que
le cavalier ne peut pas atteindre plus de
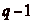 classes, ce qui sera suffisant pour
conclure la démonstration, puisqučil existe clairement des
éléments de chacune les classes dans
classes, ce qui sera suffisant pour
conclure la démonstration, puisqučil existe clairement des
éléments de chacune les classes dans
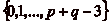 , puisque p est supposé supérieur
à 1, cčest à dire que
, puisque p est supposé supérieur
à 1, cčest à dire que 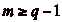 . Remarquons
tout de suite que la classe sur laquelle se trouve le cavalier
après un certain nombre de coups ne dépend que du
nombre de déplacement de p cases qučil aura fait et de leur sens, puisque la classe
ne change pas lorsque le cavalier se déplace de
q cases.
. Remarquons
tout de suite que la classe sur laquelle se trouve le cavalier
après un certain nombre de coups ne dépend que du
nombre de déplacement de p cases qučil aura fait et de leur sens, puisque la classe
ne change pas lorsque le cavalier se déplace de
q cases.
Pour pouvoir avancer de p cases, il faut se trouver dans une
case de 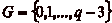 , pour
pouvoir reculer de p cases, il faut se trouver dans une
case de
, pour
pouvoir reculer de p cases, il faut se trouver dans une
case de 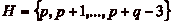 . Comme
chaque classe est représentée au plus une fois dans
. Comme
chaque classe est représentée au plus une fois dans
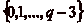 et une fois dans
et une fois dans
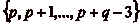 , et que tout changement de classe
nécessite un déplacement de p cases, il apparaît que si un
cavalier se trouve dans la classe de
a, un quelconque
déplacement (de
p ou de
q cases) va soit le laisser dans cette
même classe, soit lčamener dans la classe de
, et que tout changement de classe
nécessite un déplacement de p cases, il apparaît que si un
cavalier se trouve dans la classe de
a, un quelconque
déplacement (de
p ou de
q cases) va soit le laisser dans cette
même classe, soit lčamener dans la classe de
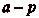 , soit lčamener dans la classe de
, soit lčamener dans la classe de
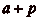 .
.
Ainsi, le cavalier en partant de la classe de 0, pourra atteindre
les classes de la forme p,
2p,, kp, où la classe de
kp est une classe qui nčest pas
représentée dans G (il en existe nécessairement
une, puisque seules 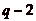 classes y
sont présentes &endash; on a donc
classes y
sont présentes &endash; on a donc
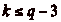 , ce qui assure que les classes sont deux
à deux distinctes), si bien qučelle nčest pas liée
à la classe de
, ce qui assure que les classes sont deux
à deux distinctes), si bien qučelle nčest pas liée
à la classe de 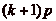 (on ne peut
pas avancer de p cases en partant dčune case de
G). On pourra de même reculer, et
ce pour atteindre les classes de la forme
(on ne peut
pas avancer de p cases en partant dčune case de
G). On pourra de même reculer, et
ce pour atteindre les classes de la forme
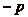 ,
,  ,,
,,
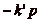 . Mais comme pour tout
. Mais comme pour tout 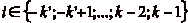 , les
classes de ip et de
, les
classes de ip et de
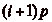 sont liées, cela signifie que pour
tout
sont liées, cela signifie que pour
tout 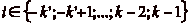 , la classe de
ip est
représentée dans
G, ce qui implique que
le nombre de classes que le cavalier peut atteindre est égal
au nombre de cases dans
G plus une (la classe
de kp), et donc que le cavalier ne peut
atteindre que
, la classe de
ip est
représentée dans
G, ce qui implique que
le nombre de classes que le cavalier peut atteindre est égal
au nombre de cases dans
G plus une (la classe
de kp), et donc que le cavalier ne peut
atteindre que  classes, ce
qui achève la démonstration. CQFD.
classes, ce
qui achève la démonstration. CQFD.
Ainsi, pour 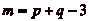 , le cavalier peut ne atteindre peut pas
atteindre les q classes, cčest à dire qučil ne
peut pas passer par toutes les cases.
, le cavalier peut ne atteindre peut pas
atteindre les q classes, cčest à dire qučil ne
peut pas passer par toutes les cases.
La plus petite valeur possible pour m est donc
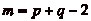 , ce qui correspond à une bande de
, ce qui correspond à une bande de
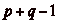 cases.
cases.
VI.
Le cas
bidimensionnel
On peut également se poser la question suivante (qui va
expliquer le titre de lčexposé) : on se donne un
« cavalier » qui se déplace sur un
échiquier  selon des
pas de p cases dans un sens, suivies de pas de
q cases dans une direction
perpendiculaire. Dans le cas du cavalier du jeu dčéchecs, on a
ainsi
selon des
pas de p cases dans un sens, suivies de pas de
q cases dans une direction
perpendiculaire. Dans le cas du cavalier du jeu dčéchecs, on a
ainsi 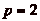 et
et 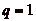 . On demande quelle est la plus petite
valeur de m telle que
le cavalier, en partant dčun case quelconque du lčéchiquier,
puisse atteindre toutes les cases de celui-ci.
. On demande quelle est la plus petite
valeur de m telle que
le cavalier, en partant dčun case quelconque du lčéchiquier,
puisse atteindre toutes les cases de celui-ci.
Nous nčavons pas entièrement résolu ce
problème. Toutefois, nous avons dégagé quelques
minorations intéressantes. On supposera ici aussi, par
symétrie, que 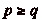 . En revanche, on nčaura pas
nécessairement
. En revanche, on nčaura pas
nécessairement 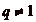 .
.
Tout dčabord, on peut remarquer que lčabscisse du cavalier varie
à chaque mouvement ou de
p, ou de
q. Si le cavalier passe
par toutes les cases, alors son abscisse prendra aussi toutes les
valeurs de 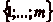 , ce qui
nous ramène au problème précédent,
à une unité près (puisque lors du
problème initial, la bande de déplacement étant
numérotée à partir de 0, et ici, à partir
de 1). On a donc nécessairement
, ce qui
nous ramène au problème précédent,
à une unité près (puisque lors du
problème initial, la bande de déplacement étant
numérotée à partir de 0, et ici, à partir
de 1). On a donc nécessairement
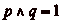 , et
, et 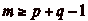 .
.
Dčautre part, lorsque le cavalier se trouve sur la case
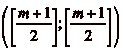 (où [] désigne la partie
entière), il doit pouvoir faire au moins un
déplacement. Si lčon ne tient pas compte des problèmes
de borne, les 8 cases atteignables par le cavalier sont celles de
coordonnées
(où [] désigne la partie
entière), il doit pouvoir faire au moins un
déplacement. Si lčon ne tient pas compte des problèmes
de borne, les 8 cases atteignables par le cavalier sont celles de
coordonnées 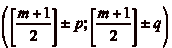 et
et 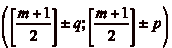 . Au moins
lčune dčentre elles appartient à
. Au moins
lčune dčentre elles appartient à
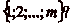 , dčoù
, dčoù 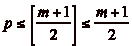 ou
ou
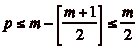 .
.
On a donc nécessairement 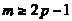 , ce qui est plus fort que la
minoration précédente, mais ne nous aurait pas fourni
la condition
, ce qui est plus fort que la
minoration précédente, mais ne nous aurait pas fourni
la condition 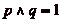 .
.
***
MOTS
CLEFS SAUTS DE
CAVALIER PGCD VECTEURS ENTIERS COMBINAISON LINÉAIRE FROBENIUS
Comptes
Rendus MATh.enJEANS, 04-04
©MATH.enJEANS, 2005
![]() ), en avant ou en
arrière. On place sur cette demi-droite un mur, auquel
correspond le numéro m (
), en avant ou en
arrière. On place sur cette demi-droite un mur, auquel
correspond le numéro m (![]() ), qui empêche le cavalier de passer
par une quelconque case dont le numéro est strictement
supérieur à celui du mur.
), qui empêche le cavalier de passer
par une quelconque case dont le numéro est strictement
supérieur à celui du mur.![]() , où
on a trivialement
, où
on a trivialement ![]()
![]() (
(![]() Z), donc
divisible par
Z), donc
divisible par ![]() . On doit
donc avoir, si lčon veut atteindre toutes les cases,
. On doit
donc avoir, si lčon veut atteindre toutes les cases,
![]() .
.![]() et que
et que
![]() dans la suite de
lčexposé.
dans la suite de
lčexposé.![]() convient.
convient.![]() , il existe
, il existe
![]() tels que
tels que
![]() .
.![]() Z tels que
Z tels que
![]() , soit, pour tout
, soit, pour tout ![]() Z,
Z,
![]() .
.![]() et
et ![]() , il faut et suffit que
, il faut et suffit que ![]() . Or, il
existe toujours un entier dans lčintervalle
. Or, il
existe toujours un entier dans lčintervalle
![]() , puisqučil est dčamplitude
, puisqučil est dčamplitude
![]() .
.![]() , il existe donc
, il existe donc
![]() tels que
tels que ![]() , et la case
x peut donc être atteinte par le
cavalier qui, en faisant
, et la case
x peut donc être atteinte par le
cavalier qui, en faisant ![]() pas de p cases en avant et
pas de p cases en avant et
![]() pas de
q cases en avant,
arrive sur la case souhaitée en passant par des cases de
numéros croissants, et donc ne dépasse pas le mur, dont
le numéro est supérieur ou égal à celui
de la case que lčon souhaite atteindre.
pas de
q cases en avant,
arrive sur la case souhaitée en passant par des cases de
numéros croissants, et donc ne dépasse pas le mur, dont
le numéro est supérieur ou égal à celui
de la case que lčon souhaite atteindre.![]() ,
, ![]() le quotient et
le quotient et ![]() le reste
de la division euclidienne de
le reste
de la division euclidienne de ![]() par
par ![]() . On a
. On a
![]() ,
dčoù
,
dčoù![]()
![]() . On a
. On a ![]() , donc
, donc ![]() est atteignable. On peut donc
atteindre la case x en se
rendant dčabord sur la case
est atteignable. On peut donc
atteindre la case x en se
rendant dčabord sur la case ![]() , puis en reculant de
, puis en reculant de
![]() fois de
fois de ![]() , et ce
quelque soit
, et ce
quelque soit ![]() . Comme on
peut aussi atteindre les cases de
E,
. Comme on
peut aussi atteindre les cases de
E, ![]() convient
donc (puisque
convient
donc (puisque ![]() ).
m existe donc. CQFD.
).
m existe donc. CQFD.![]() (puisque pour atteindre toutes les cases de
(puisque pour atteindre toutes les cases de
![]() , il faut faire au moins un
déplacement).
, il faut faire au moins un
déplacement).![]() et
r le reste de la division euclidienne de n par
et
r le reste de la division euclidienne de n par
![]() .
. ![]() , donc la
case r est atteignable sans dépasser
le mur placé en mč. Pour atteindre la case
n sans dépasser ce même
mur, il suffit dčaller en r, puis dčavancer du bon nombre de fois
de
, donc la
case r est atteignable sans dépasser
le mur placé en mč. Pour atteindre la case
n sans dépasser ce même
mur, il suffit dčaller en r, puis dčavancer du bon nombre de fois
de ![]() cases.
CQFD.
cases.
CQFD.![]() .
.![]()
![]() .
.![]() en partant de la case 0, on peut aussi le
faire en partant de nčimporte quelle case de
en partant de la case 0, on peut aussi le
faire en partant de nčimporte quelle case de
![]() . En effet, il suffit pour cela de se rendre
de la case de départ à la case 0 (en suivant le chemin
inverse de celui que le cavalier suit pour aller de la case 0
à la case de départ), à partir de laquelle il
est possible de se rendre sur nčimporte quelle case de
. En effet, il suffit pour cela de se rendre
de la case de départ à la case 0 (en suivant le chemin
inverse de celui que le cavalier suit pour aller de la case 0
à la case de départ), à partir de laquelle il
est possible de se rendre sur nčimporte quelle case de
![]() (par hypothèse).
(par hypothèse).![]() , demandons au cavalier,
initialement placé sur la case
, demandons au cavalier,
initialement placé sur la case
![]() , de réaliser le parcours
suivant : sčil peut reculer de q cases ou avancer de p cases, il le fait (les deux ne sont
pas possibles simultanément, puisque la longueur de segment
qučil peut parcourir est de
, de réaliser le parcours
suivant : sčil peut reculer de q cases ou avancer de p cases, il le fait (les deux ne sont
pas possibles simultanément, puisque la longueur de segment
qučil peut parcourir est de ![]() cases),
sinon il sčarrête.
cases),
sinon il sčarrête.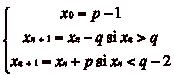
![]() , le cavalier sčarrête.
, le cavalier sčarrête.![]() , et
seulement celles-ci.
, et
seulement celles-ci.![]() est
à valeurs dans
est
à valeurs dans ![]() , et que
pour tout n pour lequel
, et que
pour tout n pour lequel
![]() est défini, il existe
est défini, il existe
![]() tels que
tels que ![]() et
et
![]() , le cavalier ne faisant que
des déplacements de
p cases en avant et des
déplacements de
q cases en
arrière.
, le cavalier ne faisant que
des déplacements de
p cases en avant et des
déplacements de
q cases en
arrière.![]() (
(![]() ) distincts tels que
) distincts tels que
![]() et que
et que ![]() soit
minimum. Alors la suite prend des valeurs deux à deux
distinctes pour des indices compris (au sens large) entre
i et
soit
minimum. Alors la suite prend des valeurs deux à deux
distinctes pour des indices compris (au sens large) entre
i et
![]() , par hypothèse de
minimalité sur
, par hypothèse de
minimalité sur ![]() . Comme la
suite est à valeurs dans
. Comme la
suite est à valeurs dans ![]() , on a donc
, on a donc ![]() (
(![]() est lčensemble des valeurs que peut prendre
la suite, au nombre de m ; or, entre
xi et
est lčensemble des valeurs que peut prendre
la suite, au nombre de m ; or, entre
xi et
![]() , la suite prend par hypothèse des
valeurs deux à deux distinctes, au nombre de
, la suite prend par hypothèse des
valeurs deux à deux distinctes, au nombre de ![]() ).
).
![]() tels que
tels que
![]() et
et ![]() , ainsi que
, ainsi que
![]() et
et
![]() , soit
, soit
![]() , dčoù
, dčoù
![]() et
et
![]() . On a aussi
. On a aussi ![]() et
et
![]() , puisque
, puisque
![]() . p et q
étant supposés premiers entre eux, dčaprès le
théorème de Gauss, on a
. p et q
étant supposés premiers entre eux, dčaprès le
théorème de Gauss, on a ![]() et
et
![]() . Dčautre part, si
. Dčautre part, si ![]() , alors
lčégalité
, alors
lčégalité ![]() entraîne clairement
entraîne clairement ![]() , soit
, soit
![]() , ce qui est exclu par
hypothèse. Donc
, ce qui est exclu par
hypothèse. Donc ![]() , et, de même,
, et, de même, ![]() . On a donc
. On a donc
![]() et
et
![]() , dčoù
, dčoù
![]() , ce qui est absurde.
, ce qui est absurde.